题目内容
10.解下列关于x的方程:(1)log2(2x+1)=log2(3x);
(2)log5(2x+1)=log5(x2-2).
分析 根据对数的定义即可求出,注意真数大于0.
解答 解:(1)log2(2x+1)=log2(3x),
∴2x+1=3x,
解得x=1,
(2)log5(2x+1)=log5(x2-2),
∴$\left\{\begin{array}{l}{2x+1>0}\\{{x}^{2}-2>0}\\{2x+1={x}^{2}-2}\end{array}\right.$,
解得x=3.
点评 本题考查了对数的定义和方程的解法,关键是注意对数函数的定义域,属于基础题.

练习册系列答案
相关题目
1.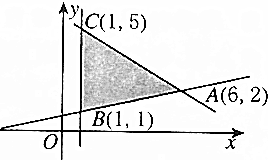 给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
 给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{5}{3}$ |
15.若logx$\root{7}{y}$=z,则( )
| A. | y7=xz | B. | y=x7z | C. | y=7•xz | D. | x=z7y |