题目内容
四面体ABCD中，已知AB=CD=
，AC=BD=
，AD=BC=
，则四面体ABCD的外接球的表面积为 ．
| 29 |
| 34 |
| 37 |
考点：球内接多面体,球的体积和表面积
专题：空间位置关系与距离
分析：将四面体补成长方体，通过求解长方体的对角线就是球的直径，然后求解外接球的表面积．
解答：
解：由题意可采用割补法，考虑到四面体ABCD的四个面为全等的三角形，
所以可在其每个面补上一个以
，
，
为三边的三角形作为底面，
且以分别x，y，z长、两两垂直的侧棱的三棱锥，
从而可得到一个长、宽、高分别为x，y，z的长方体，
并且x2+y2=29，x2+z2=34，y2+z2=37，
则有（2R）2=x2+y2+z2=50（R为球的半径），
所以球的表面积为S=4πR2=50π．
故答案为：50π
所以可在其每个面补上一个以
| 29 |
| 34 |
| 37 |
且以分别x，y，z长、两两垂直的侧棱的三棱锥，
从而可得到一个长、宽、高分别为x，y，z的长方体，
并且x2+y2=29，x2+z2=34，y2+z2=37，
则有（2R）2=x2+y2+z2=50（R为球的半径），
所以球的表面积为S=4πR2=50π．
故答案为：50π
点评：本题考查几何体的外接球的表面积的求法，割补法的应用，判断外接球的直径是长方体的对角线的长是解题的关键之一．
练习册系列答案
相关题目
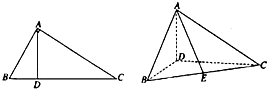如图，在△ABC中，AB⊥AC，AD⊥BC，∠ABC=
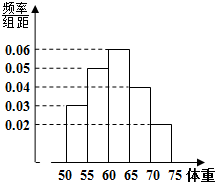某公司为了了解员工们的健康状况，随机抽取了部分员工作为样本，测量他们的体重（单位：公斤），体重的分组区间为[50，55），[55，60），[60，65），[65，70），[70，75]，由此得到样本的频率分布直方图，如图所示．根据频率分布直方图，估计该公司员工体重的众数是