题目内容
15.如图,在正方体ABCD-A1B1C1D1中,AB=1,DD1中点为Q,过A、Q、B1三点的截面面积为$\frac{9}{8}$.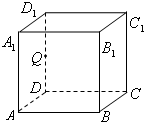
分析 根据题意,画出图形,得出过A、Q、B1三点的截面为等腰梯形,结合图中数据即可求出截面的面积.
解答 解:如图所示,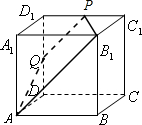
取C1D1的中点P,连接PQ、PB1、AB1和AQ,则四边形AB1PQ是过A、Q、B1三点的截面;
∵PQ∥C1D,且PQ=$\frac{1}{2}$C1D,
∴PQ∥AB1,
∴四边形AB1PQ是梯形;
∵AB=1,
∴AB1=$\sqrt{2}$,PQ=$\frac{\sqrt{2}}{2}$;
且梯形的高为$\sqrt{{1}^{2}{+(\frac{1}{2})}^{2}{-(\frac{1}{2}×\frac{1}{2}\sqrt{2})}^{2}}$=$\frac{3}{2\sqrt{2}}$,
∴截面面积为$\frac{1}{2}$×($\frac{\sqrt{2}}{2}$+$\sqrt{2}$)×$\frac{3}{2\sqrt{2}}$=$\frac{9}{8}$.
故答案为:$\frac{9}{8}$.
点评 本题考查了空间几何体中的线、面之间的位置关系的应用问题,是综合性题目.

练习册系列答案
相关题目
5.已知 a1=3,a2=6,且 an+2=an+1-an,则a2011=( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
10.若a是函数f(x)=3x-log${\;}_{\frac{1}{3}}$x的零点,且f(b)<0,则( )
| A. | 0<b<a | B. | 0<a<b | C. | a=b | D. | a≤b |
 在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABCF是BC的中点,AB=AC=BE=2,CD=1.求证:
在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABCF是BC的中点,AB=AC=BE=2,CD=1.求证: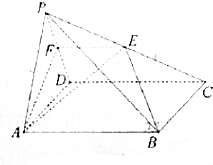 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.