题目内容
17.已知函数f(x)=sin$\frac{π}{2}$x-1(x<0),g(x)=logax(a>0且a≠1 ).若它们的图象上存在关于y轴对称的点至少有3对,则实数a的取值范围是( )| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | ($\frac{\sqrt{5}}{5}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
分析 求出函数f(x)=sin$\frac{π}{2}$x-1,(x<0)关于y轴对称的解析式,利用数形结合即可得到结论.
解答  解:若x>0,则-x<0,∵x<0时,f(x)=sin($\frac{π}{2}$x)-1,
解:若x>0,则-x<0,∵x<0时,f(x)=sin($\frac{π}{2}$x)-1,
∴f(-x)=sin(-$\frac{π}{2}$x)-1=-sin($\frac{π}{2}$x)-1,
则若f(x)=sin($\frac{π}{2}$x)-1(x<0)的图象关于y轴对称,
则f(-x)=-sin($\frac{π}{2}$x)-1=f(x),即y=-sin($\frac{π}{2}$x)-1,x>0.
设g(x)=-sin($\frac{π}{2}$x)-1,x>0,作出函数g(x)的图象,
要使y=-sin($\frac{π}{2}$x)-1,x>0与f(x)=logax,x>0的图象至少有3个交点,
则0<a<1且满足g(5)<f(5),即-2<loga5,即loga5>logaa-2,
则5<$\frac{1}{{a}^{2}}$,∴0<a<$\frac{\sqrt{5}}{5}$,
故选:A.
点评 本题主要考查分段函数的应用,作出函数关于y对称的图象,利用数形结合的思想是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
7.如图为某市2017年2月28天的日空气质量指数折线图.
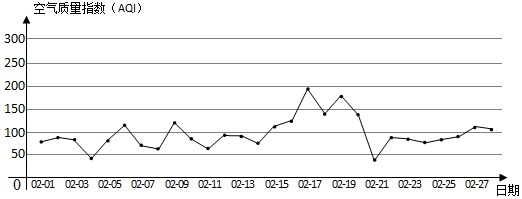
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
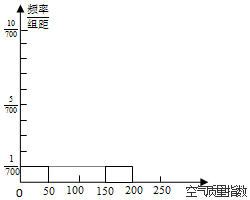
(Ⅰ)请根据所给的折线图补全下方的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)研究人员发现,空气质量指数测评中PM2.5与燃烧排放的CO两个项目存在线性相关关系,以100ug/m3为单位,如表给出PM2.5与CO的相关数据:
求y关于x的回归方程,并估计当CO排放量是200ug/m3时,PM2.5的值.
(用最小二乘法求回归方程的系数是$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$)

由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |

(Ⅱ)研究人员发现,空气质量指数测评中PM2.5与燃烧排放的CO两个项目存在线性相关关系,以100ug/m3为单位,如表给出PM2.5与CO的相关数据:
| CO(x) | 0.5 | 1 | 1.5 |
| PM2.5(y) | 1 | 2 | 4 |
(用最小二乘法求回归方程的系数是$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n•{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$)
