题目内容
8.已知$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,且|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2.求:(1)($\overrightarrow{a}$-2$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$);
(2)|3$\overrightarrow{a}$-4$\overrightarrow{b}$|.
分析 先根据向量的数量积公式求出$\overrightarrow{a}$•$\overrightarrow{b}$=-4,再分别根据向量的数量积的运算和模计算即可.
解答 解:$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,且|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos120°=4×2×(-$\frac{1}{2}$)=-4,
(1)($\overrightarrow{a}$-2$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=|$\overrightarrow{a}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{b}$-2|$\overrightarrow{b}$|2=16+4-2×4=12;
(2)|3$\overrightarrow{a}$-4$\overrightarrow{b}$|2=9|$\overrightarrow{a}$|2-24$\overrightarrow{a}$•$\overrightarrow{b}$+16|$\overrightarrow{b}$|2=9×42-24×(-4)+16×22=16×19,
∴|3$\overrightarrow{a}$-4$\overrightarrow{b}$|=4$\sqrt{19}$.
点评 本题考查了向量的数量积公式和向量的模,属于基础题.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{3}+\frac{1}{3}i$ | C. | $\frac{2}{3}-\frac{1}{3}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{12}$或$\frac{5π}{12}$ |
| A. | {x|x<0} | B. | {x|x>1} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
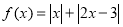 ,
,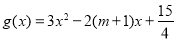 ;
;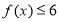 的解集;
的解集;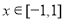 ,
,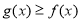 ,求
,求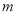 的取值范围.
的取值范围. 如图,边长为2的正方形内有一不规则阴影部分,随机向正方形内投入200粒芝麻,恰好60粒落入阴影部分,则不规则图形的面积为1.2.
如图,边长为2的正方形内有一不规则阴影部分,随机向正方形内投入200粒芝麻,恰好60粒落入阴影部分,则不规则图形的面积为1.2.