题目内容
给出下列4个命题:①若 ,则
,则 是等腰三角形;②若
是等腰三角形;②若 ,则
,则 是直角三角形;③若
是直角三角形;③若 ,则
,则 是钝角三角形;④若
是钝角三角形;④若 ,则
,则 是等边三角形.其中正确的命题是( )
是等边三角形.其中正确的命题是( )
| A.①③ | B.③④ | C.①④ | D.②③ |
B
解析试题分析:①若sin2A=sin2B,则 2A=2B,或 2A+2B=π,即A="B" 或C=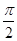 ,故△ABC为等腰三角形 或直角三角形,故①不正确.
,故△ABC为等腰三角形 或直角三角形,故①不正确.
②若sinA=cosB,不能推出△ABC是直角三角形,如A=B=45°时,虽有sinA=cosB,但△ABC不是直角三角形,故②不正确.
③若cosA•cosB•cosC<0,则由三角形各个内角的范围及内角和等于180° 知,cosA、cosB、cosC两个是正实数,一个是负数,故A、B、C中两个是锐角,一个是钝角,故③正确.
④若cos(A-B)•cos(B-C)•cos(C-A)=1,则由三角形各个内角的范围及内角和等于180° 知,
cos(A-B)=cos(B-C)=cos(C-A)=1,故有 A=B=C,故△ABC是等边三角形,故④正确.
即③④正确,故选B.
考点:和差的三角函数公式,三角形的特征。
点评:典型题,本题较综合的考察三角形的基本特征以及和差的三角函数公式,属于中档题。

练习册系列答案
相关题目
已知a,b是实数,则“| a+b |=| a |+| b |”是“ab>0”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若命题 ,则
,则 :( )
:( )
A. | B. |
C. | D.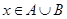 |
“三角形有一个内角为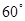 ”是“三内角成等差数列”的( )
”是“三内角成等差数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设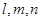 均为直线,其中
均为直线,其中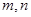 在平面
在平面 内,则
内,则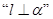 是
是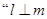 且
且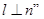 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下面是关于复数 的三个命题:
的三个命题: 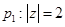
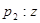 在复平面内对应的点在第四象限
在复平面内对应的点在第四象限 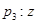 是纯虚数
是纯虚数
其中的真命题为
A.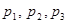 | B.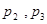 | C.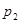 | D.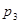 |
“函数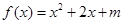 存在零点”的一个必要不充分条件是( )
存在零点”的一个必要不充分条件是( )
A.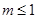 | B.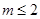 | C.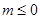 | D.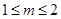 |
 ,集合
,集合 ,则
,则 是“
是“ ”( )
”( )
 ,则方程
,则方程
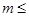 0”.
0”.

