题目内容
设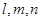 均为直线,其中
均为直线,其中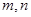 在平面
在平面 内,则
内,则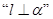 是
是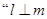 且
且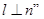 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:因为,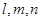 均为直线,
均为直线, 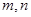 在平面
在平面 内,所以,
内,所以,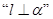 时,
时,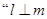 且
且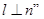 ;反之,
;反之,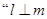 且
且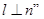 ,不一定有
,不一定有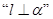 ,因为,m,n不一定是相交直线。故选A。
,因为,m,n不一定是相交直线。故选A。
考点:立体几何的垂直关系,充要条件的概念。
点评:简单题,充要条件的判断问题,往往综合性较强,需要综合应用数学知识加以处理,本题主要利用立体几何的垂直关系。

练习册系列答案
相关题目
设集合 ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
给出下列4个命题:①若 ,则
,则 是等腰三角形;②若
是等腰三角形;②若 ,则
,则 是直角三角形;③若
是直角三角形;③若 ,则
,则 是钝角三角形;④若
是钝角三角形;④若 ,则
,则 是等边三角形.其中正确的命题是( )
是等边三角形.其中正确的命题是( )
| A.①③ | B.③④ | C.①④ | D.②③ |
设 是空间两条直线,
是空间两条直线, 是空间一个平面.当
是空间一个平面.当 时,“
时,“ ”是“
”是“ ”的
”的
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
给出四个命题:①函数是其定义域到值域的映射;②f(x)=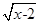 +
+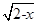 是函数;③函数y=2x(x∈N)的图象是一条直线;④f(x)=
是函数;③函数y=2x(x∈N)的图象是一条直线;④f(x)=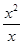 与g(x)=x是同一个函数.其中正确的有 ( )
与g(x)=x是同一个函数.其中正确的有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知 是可导函数,“
是可导函数,“ ”是“
”是“ 为函数
为函数 极值点”的( )
极值点”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“φ=π”是“曲线y=sin(2x+φ)过坐标原点的” ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
| A.若f(x) 是偶函数,则f(-x)是偶函数 |
| B.若f(x)不是奇函数,则f(-x)不是奇函数 |
| C.若f(-x)是奇函数,则f(x)是奇函数 |
| D.若f(-x)不是奇函数,则f(x)不是奇函数 |
 R,则a>2是(a-1)(a-2)>0的
R,则a>2是(a-1)(a-2)>0的