题目内容
【题目】已知函数![]() 在点
在点![]() 处的切线是
处的切线是![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 恒成立时,求实数
恒成立时,求实数![]() 的取值范围(
的取值范围(![]() 为自然对数的底数).
为自然对数的底数).
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意可得函数的解析式![]() (
(![]() ),则
),则![]() ,
,![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(2)原问题等价于![]() 在
在![]() 恒成立,
恒成立,
【法一】设![]() ,由题意可得
,由题意可得![]() ;
;![]() .据此有
.据此有![]() ,解得
,解得![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .
.
【法二】设![]() (
(![]() ),则
),则![]() ,
,
结合导函数的解析式可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.所以
上单调递减.所以![]() ,即
,即![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)因为![]() ,所以
,所以![]() ,
,
因为点![]() 处的切线是
处的切线是![]() ,所以
,所以![]() ,且
,且![]()
所以![]() ,即
,即![]() (
(![]() )
)
所以![]() ,所以在
,所以在![]() 上递增,在
上递增,在![]() 上递减
上递减
所以![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(2)当![]() 在
在![]() 恒成立时,由(1)
恒成立时,由(1)![]() ,
,
即![]() 在
在![]() 恒成立,
恒成立,
【法一】设![]() ,则
,则![]() ,
,![]() ,
,
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() ;
;
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() .
.
所以![]() 均在
均在![]() 处取得最值,所以要使
处取得最值,所以要使![]() 恒成立,
恒成立,
只需![]() ,即
,即![]() ,解得
,解得![]() ,又
,又![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
【法二】设![]() (
(![]() ),则
),则![]()
当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ,
,![]() ,即
,即![]()
当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ,
,![]() ,即
,即![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() ,即
,即![]() ,又
,又![]()
所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】交管部门为宣传新交规举办交通知识问答活动,随机对该市![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题统计结果如图表所示:
人,回答问题统计结果如图表所示:
分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
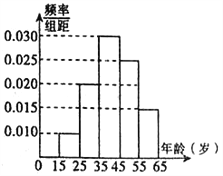
(1)分别求出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)从第![]() ,
,![]() ,
,![]() 组回答正确的人中用分层抽样方法抽取
组回答正确的人中用分层抽样方法抽取![]() 人,则第
人,则第![]() ,
,![]() ,
,![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求:所抽取的
人颁发幸运奖,求:所抽取的![]() 人中至少有一个第
人中至少有一个第![]() 组的人的概率.
组的人的概率.