题目内容
4．已知tanα=2，则$\frac{4sinα-2cosα}{3cosα+3sinα}$=$\frac{2}{3}$．分析 原式分子分母同时除以cosα，利用同角三角函数间的基本关系化简，将已知等式代入计算即可求出值．
解答 解：∵tanα=2，
∴原式=$\frac{4tanα-2}{3+3tanα}$=$\frac{8-2}{3+6}$=$\frac{2}{3}$，
故答案为：$\frac{2}{3}$．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
19．某市电子认证审查流程图如图：
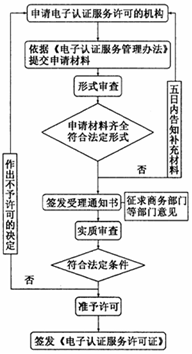
则有几处审查可能不被通过的环节（ ）
则有几处审查可能不被通过的环节（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 0 |
13．在国乒“直通莫斯科”比赛中共有女运动员5人，从这10名运动员中选出6人进行男女混合双打比赛，由于排名世界第一，男队的马龙，女队的丁宁自动入选，组队方案有（ ）
| A． | ${（A_5^2）^2}$ | B． | ${（C_4^2）^2}A_2^2$ | C． | ${（C_5^2）^2}A_3^3$ | D． | ${（C_4^2）^2}A_3^3$ |