题目内容
直线x-y+2=0与圆x2+y2=4的位置关系是 ．（填相交、相切或相离）
考点：直线与圆的位置关系
专题：直线与圆
分析：求出圆的圆心与直线的距离与半径比较，即可判断直线与圆的位置关系．
解答：
解：直线x-y+2=0与圆x2+y2=4的圆心的距离为：d=
=
＜2，
直线x-y+2=0与圆x2+y2=4的位置关系是相交．
故答案为：相交．
| 2 | ||
|
| 2 |
直线x-y+2=0与圆x2+y2=4的位置关系是相交．
故答案为：相交．
点评：本题考查直线与圆的位置关系的应用，圆心到直线的距离与半径比较是解题的关键．
练习册系列答案
相关题目
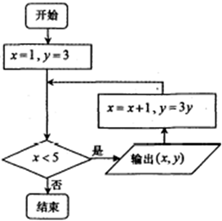运行如图所示的程序框图，输出的所有实数对（x，y）所对应的点都在某函数图象上，则该函数的解析式为（ ）| A、y=x+2 | ||
B、y=
| ||
| C、y=3x | ||
| D、y=3x3 |
已知定义在R上的奇函数f（x）满足f（2+x）=f（-x），当0≤x≤1时，f（x）=x2，则f（2015）=（ ）
| A、-1 |
| B、1 |
| C、0 |
| D、20152 |
如图是一个算法流程图，则输出的x的值是