题目内容
19.已知两点$A(\sqrt{3},0),C(-\sqrt{3},0)$,若一动点Q在运动过程中总满足|AQ|+|CQ|=4,O为坐标原点.(1)当点P在圆上运动时,求点Q的轨迹E的方程.
(2)设过点B(0,-2)的直线与E交于M,N两点,当△OMN的面积为1时,求此直线的方程.
分析 (1)由椭圆定义知Q点的轨迹是椭圆,由此能求出点Q的轨迹E的方程.
(2)设直线为:y=kx-2,将y=kx-2代入椭圆方程,(1+4k2)x2-16kx+12=0.由此利用根的判断式、韦达定理、弦长公式,结合已知条件能求出直线方程.
解答 解:(1)由题意知|PQ|=|AQ|,又∵|CP|=|CQ|+|PQ|=4…(2分)
∴|CQ|+|AQ|=4》|AC|=2$\sqrt{3}$,
由椭圆定义知Q点的轨迹是椭圆,…(4分)
2a=4,即a=2,2c=2$\sqrt{3}$,即c=$\sqrt{3}$,
∴b2=4-3=1,
∴点Q的轨迹E的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.…(6分)
(2)由题意知所求的直线不可能垂直于x轴,所以可设直线为:y=kx-2,…(7分)
M(x1,y1),N(x2,y2),
将y=kx-2代入$\frac{x^2}{4}+{y^2}=1中得$(1+4k2)x2-$16kx+12=0,△>0得{k^2}>\frac{3}{4}$.
∴${x_1}+{x_2}=\frac{16k}{{1+4{k^2}}},{x_1}{x_2}=\frac{12}{{1+4{k^2}}}$…(8分)
$又∵{S_{△OMN}}=\frac{1}{2}•|{OB}|•$|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{4\sqrt{4{k}^{2}-3}}{1+4{k}^{2}}$=1.…(10分)
解得k=$±\frac{\sqrt{7}}{2}$,满足△>0.∴$所求的直线方程为y=±\frac{{\sqrt{7}}}{2}x$-2.…(12分)
点评 本题考查点的轨迹方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意根的判断式、韦达定理、弦长公式的合理运用.

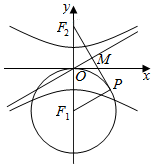 如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )
如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
| A. | 5,15,10 | B. | 3,18,9 | C. | 7,13,10 | D. | 5,16,9 |
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$-1 | D. | $\sqrt{2}$-1 |