题目内容
14.已知抛物线y2=2px的焦点为F,准线方程是x=-1.(I)求此抛物线的方程;
(Ⅱ)设点M在此抛物线上,且|MF|=3,若O为坐标原点,求△OFM的面积.
分析 (I)利用准线方程是x=-1,求此抛物线的方程;
(Ⅱ)设点M在此抛物线上,且|MF|=3,利用抛物线的定义求出M的坐标,即可求△OFM的面积.
解答 解:(Ⅰ)因为抛物线的准线方程为x=-1,
所以$\frac{p}{2}=1$…(2分)
得p=2…(4分)
所以,抛物线的方程为 y2=4x…(5分)
(Ⅱ)设M(x0,y0),因为点M(x0,y0)在抛物线上,且|MF|=3,
由抛物线定义知|MF|=x0+$\frac{p}{2}$=3…(8分)
得x0=2…(10分)
由M(2,y0)在抛物线上,满足抛物线的方程为y2=4x知y0=±2$\sqrt{2}$…(12分)
所以△OMP的面积为$\frac{1}{2}|OF|$|y0|=$\frac{1}{2}×1×2\sqrt{2}$=$\sqrt{2}$.…(14分)
点评 本题考查抛物线的方程与定义,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.等差数列{an}的前n项和为Sn,若S3=6,a1=4,则S5等于( )
| A. | -2 | B. | 0 | C. | 5 | D. | 10 |
3.过三点A(1,2),B(3,-2),C(11,2)的圆交x轴于M,N两点,则|MN|=( )
| A. | $3\sqrt{6}$ | B. | $4\sqrt{6}$ | C. | $\sqrt{21}$ | D. | $2\sqrt{21}$ |
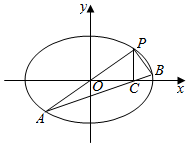 如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.
如图,过坐标原点O的直线椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于P,A两点,其中P在第一象限,B在椭圆Г上,直线AB与x轴交于点C.