题目内容
8.函数y=$\frac{\sqrt{5x+3}}{x}$的定义域区间为{x|x≥-$\frac{3}{5}$且x≠0}.分析 根据函数y的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答 解:∵函数y=$\frac{\sqrt{5x+3}}{x}$,
∴$\left\{\begin{array}{l}{5x+3≥0}\\{x≠0}\end{array}\right.$,
解得x≥-$\frac{3}{5}$且x≠0;
∴函数y的定义域区间为{x|x≥-$\frac{3}{5}$且x≠0}.
故答案为:{x|x≥-$\frac{3}{5}$或x≠0}.
点评 本题考查了根据函数的解析式求定义域的应用问题,是基础题目.

练习册系列答案
相关题目
3.已知a、b为不等于0的实数,则$\frac{a}{b}$>1是a>b的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件. |
20.下列不能产生随机数的是( )
| A. | 抛掷骰子试验 | |
| B. | 抛硬币 | |
| C. | 计算器 | |
| D. | 正方体的六个面上分别写有1,2,2,3,4,5,抛掷该正方体 |
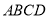 和直角梯形
和直角梯形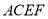 所在的平面互相垂直,其中
所在的平面互相垂直,其中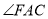 为直角,
为直角,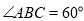 ,
,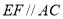 ,
,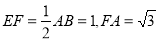 .
.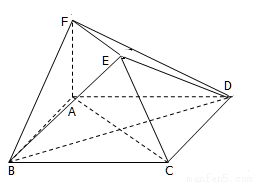
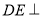 平面
平面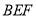 ;
;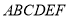 的体积.
的体积.