��Ŀ����
14����֪ƽ��ֱ������ϵxOy�У����ڵ�P��x0��y0����ֱ��l��ax+by+c=0�����dzƦ�=$\frac{a{x}_{0}+b{y}_{0}+c}{\sqrt{{a}^{2}+{b}^{2}}}$Ϊ��P��x0��y0����ֱ��l��ax+by+c=0�ķ�����룮��1������Բ$\frac{{x}^{2}}{4}$+y2=1�ϵ�����һ��P��x��y����ֱ��l��x-2y=0��l��x+2y=0�ķ������ֱ�Ϊ��1����2�����1��2��ȡֵ��Χ��
��2�����E��-t��0����F��t��0����ֱ��l��xcos��+2ysin��-2=0�ķ��̾���ֱ�Ϊ��1����2�������Ƿ����ʵ��t��������Ħ����Ц�1��2=1������������ڣ����t��ֵ���������ڣ�˵�����ɣ�
��3����ֱ֪��l��mx-y+n=0����ԲH��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������ԲH����������F1��F2��ֱ��l�ķ������ֱ�Ϊ��1����2�������1��2��b2����ֱ��l��x��Ľ���ΪA����y��Ľ���ΪB���ԱȽ�|AB|�ij���a+b�Ĵ�С��
���� ��1����P��x��y��Ϊ��2cos����sin������0�ܦ���2�У����¶�����æ�1����2�����ɶ����ǵ����ҹ�ʽ��������Һ�����ֵ�ɵõ�����Χ��
��2�����¶���ɵ�Ϊ��1����2���������t����Ϻ��ʽ��֪ʶ��ͬ�ǵ�ƽ����ϵ���ɵ�t��ֵ��
��3�����¶���ɵæ�1����2�������1��2��b2�����������ɵ�n2��b2+m2a2����������ľ��빫ʽ�����|AB|2=$\frac{{n}^{2}}{{m}^{2}}$+n2�����ò���ʽ�����ʺͻ�������ʽ�����ɵõ���С��ϵ��
��� �⣺��1����P��x��y��Ϊ��2cos����sin������0�ܦ���2�У�
������ɵæ�1=$\frac{x-2y}{\sqrt{1+4}}$����2=$\frac{x+2y}{\sqrt{1+4}}$��
����1��2=$\frac{{x}^{2}-4{y}^{2}}{5}$=$\frac{4co{s}^{2}��-4si{n}^{2}��}{5}$=$\frac{4}{5}$cos2����
��-1��cos2����1���ɵæ�1��2�ķ�Χ��[-$\frac{4}{5}$��$\frac{4}{5}$]��
��2��������ɵæ�1=$\frac{-tcos��-2}{\sqrt{co{s}^{2}��+4si{n}^{2}��}}$����2=$\frac{tcos��-2}{\sqrt{co{s}^{2}��+4si{n}^{2}��}}$��
�������ʵ��t��������Ħ����Ц�1��2=1�������
����$\frac{4-{t}^{2}co{s}^{2}��}{co{s}^{2}��+4si{n}^{2}��}$=1��
��Ϊ4-t2cos2��=cos2��+4sin2��=4-3cos2����
����t2=3�����t=��$\sqrt{3}$��
�ʴ��ڣ���t=��$\sqrt{3}$��
��3�����F1��-c��0����F2��c��0����
������ɵæ�1=$\frac{-mc+n}{\sqrt{1+{m}^{2}}}$����2=$\frac{mc+n}{\sqrt{1+{m}^{2}}}$��
��1��2��b2����Ϊ$\frac{{n}^{2}-{m}^{2}{c}^{2}}{1+{m}^{2}}$��b2��
����n2-m2c2��b2+b2m2��
��Ϊn2-m2��a2-b2����b2+b2m2��
����ɵ�n2��b2+m2a2��
������ɵ�A��-$\frac{n}{m}$��0����B��0��n����
�ɵ�|AB|=$\sqrt{\frac{{n}^{2}}{{m}^{2}}+{n}^{2}}$��
��|AB|2=$\frac{{n}^{2}}{{m}^{2}}$+n2��$\frac{{b}^{2}+{m}^{2}{a}^{2}}{{m}^{2}}$+b2+m2a2��
=a2+b2+$\frac{{b}^{2}}{{m}^{2}}$+m2a2��a2+b2+2ab=��a+b��2��
����|AB|��a+b��
���� ���⿼���¶������������ã�������Բ�IJ������̵����ã��Լ����ʽ�Ľ��ۺͻ�������ʽ�����ã�������������������������е��⣮

| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | 1 | D�� | 0 |
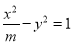 ��ʵ�᳤�������ʵ�2������m= ��
��ʵ�᳤�������ʵ�2������m= ��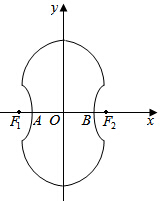 ��ͼ��ʾ�ġ�8����������������������x��ԳƵİ�Բ��һ��˫���ߵ�һ������ɵ�ͼ�Σ������ϰ��Բ����Բ������x2+y2-4y-4=0��˫���ߵ����Ҷ���A��B�Ǹ�Բ��x��Ľ��㣬˫�������Բ�ཻ����x��ƽ�е�ֱ�������˵㣮
��ͼ��ʾ�ġ�8����������������������x��ԳƵİ�Բ��һ��˫���ߵ�һ������ɵ�ͼ�Σ������ϰ��Բ����Բ������x2+y2-4y-4=0��˫���ߵ����Ҷ���A��B�Ǹ�Բ��x��Ľ��㣬˫�������Բ�ཻ����x��ƽ�е�ֱ�������˵㣮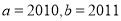 ����ʹ��
����ʹ��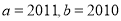 �����������ȷһ���ǣ� ��
�����������ȷһ���ǣ� ��