题目内容
10.如图是函数f(x)=Acos(ωx+φ)的一段图象,则函数f(x)图象上的最高点坐标为( )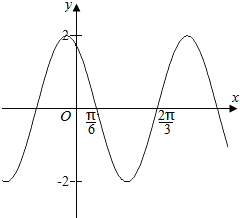
| A. | ($\frac{kπ}{2}$,2),k∈Z | B. | (kπ,2),k∈Z | C. | (2kπ-$\frac{π}{6}$,2),k∈Z | D. | (kπ-$\frac{π}{12}$,2),k∈Z |
分析 根据三角函数的图象求出A,ω和φ的值的值进行求解即可.
解答 解:由图象知A=2,函数的周期T=2×($\frac{2π}{3}-\frac{π}{6}$)=2×$\frac{π}{2}$=π,
即T=$\frac{2π}{ω}$=π,即ω=2,
则函数f(x)=2cos(2x+φ),
函数关于x=$\frac{\frac{π}{6}+\frac{2π}{3}}{2}$=$\frac{5π}{12}$对称,
即f($\frac{5π}{12}$)=2cos(2×$\frac{5π}{12}$+φ)=-2,
即cos($\frac{5π}{6}$+φ)=-1,
则$\frac{5π}{6}$+φ=π+2kπ,
即φ=$\frac{π}{6}$+2kπ,
则f(x)=2cos(2x+$\frac{π}{6}$+2kπ)=2cos(2x+$\frac{π}{6}$),
由f(x)=2cos(2x+$\frac{π}{6}$)=2,得
cos(2x+$\frac{π}{6}$)=1,即2x+$\frac{π}{6}$=2kπ,
则x=kπ-$\frac{π}{12}$,k∈Z,
即函数f(x)图象上的最高点坐标为(kπ-$\frac{π}{12}$,2),k∈Z,
故选:D
点评 本题主要考查三角函数解析式的求解以及三角函数性质的考查,根据条件求出函数的解析式是解决本题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
20.下列四种函数中,表示同一函数的是( )
| A. | y=x-1与$y=\sqrt{{{(x-1)}^2}}$ | B. | y=x2与$y={(\sqrt{x})^4}$ | C. | y=4lgx与y=2lgx2 | D. | y=x2与$y=\root{3}{x^6}$ |
18.点P(4,2)与圆x2+y2=4上任一点连线的中点轨迹方程是( )
| A. | (x+2)2+(y-1)2=1 | B. | (x-2)2+(y-1)2=1 | C. | (x-2)2+(y+1)2=1 | D. | (x+2)2+(y+1)2=1 |
2.已知过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右焦点F2的直线y=$\sqrt{3}$(x-c)与双曲线在第一象限交于点A,点F1为左焦点,且($\overrightarrow{{F}_{2}{F}_{1}}$+$\overrightarrow{{F}_{2}A}$)•$\overrightarrow{{F}_{1}A}$=0,则此双曲线的离心率为( )
| A. | $\frac{1+\sqrt{3}}{2}$ | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1+\sqrt{2}}{2}$ |