题目内容
18．点P（4，2）与圆x2+y2=4上任一点连线的中点轨迹方程是（ ）| A． | （x+2）2+（y-1）2=1 | B． | （x-2）2+（y-1）2=1 | C． | （x-2）2+（y+1）2=1 | D． | （x+2）2+（y+1）2=1 |
分析 设圆上任意一点为A，确定A与AP中点坐标之间的关系，再代入圆的方程，即可得到结论．
解答 解：设圆上任意一点为A（x1，y1），AP中点为（x，y），
则x1=2x-4，y1=2y-2
代入x2+y2=4得（2x-4）2+（2y-2）2=4，化简得（x-2）2+（y-1）2=1．
故选：B．
点评 本题考查轨迹方程，考查代入法的运用，确定坐标之间的关系是关键．
练习册系列答案
相关题目
9．下列函数中，在区间（0，1]上是增函数且最大值为-1的为（ ）
| A． | y=-x2 | B． | $y={（\frac{1}{2}）^x}$ | C． | $y=-\frac{1}{x}$ | D． | y=2x |
13．若不等式f（x）=x2+ax-2＞0在区间[1，5]上有解，且f（5）＞0，则a的取值范围是（ ）
| A． | （-$\frac{23}{5}$，+∞） | B． | [-$\frac{23}{5}$，1] | C． | （1，+∞） | D． | （-∞，-$\frac{23}{5}$] |
10．如图是函数f（x）=Acos（ωx+φ）的一段图象，则函数f（x）图象上的最高点坐标为（ ）
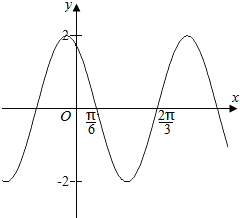
| A． | （$\frac{kπ}{2}$，2），k∈Z | B． | （kπ，2），k∈Z | C． | （2kπ-$\frac{π}{6}$，2），k∈Z | D． | （kπ-$\frac{π}{12}$，2），k∈Z |
8．现有五个球分别记为A，B，C，D，E，随机放进三个盒子，每个盒子不空，则A、B在同一盒中的概率是（ ）
| A． | $\frac{6}{25}$ | B． | $\frac{11}{25}$ | C． | $\frac{4}{15}$ | D． | $\frac{6}{15}$ |