题目内容
19．曲线y=1-$\frac{16}{81}$x2与x轴所围图形的面积是3．分析 先求出曲线与x轴的交点，设围成的平面图形面积为A，利用定积分求出A即可．
解答 解：y=1-$\frac{16}{81}$x2，令y=0得x=±$\frac{9}{4}$
设曲线y=1-$\frac{16}{81}$x2与x轴围成图形的面积为A
则A=${∫}_{-\frac{9}{4}}^{\frac{9}{4}}$（1-$\frac{16}{81}$x2）dx=（x-$\frac{16}{243}$x3）${|}_{-\frac{9}{4}}^{\frac{9}{4}}$=3
故答案为：3．
点评 考查学生利用定积分求平面图形面积的能力，解题的关键是求出积分的上下限，属于基础题．
练习册系列答案
相关题目
9．下列函数中，在区间（0，1]上是增函数且最大值为-1的为（ ）
| A． | y=-x2 | B． | $y={（\frac{1}{2}）^x}$ | C． | $y=-\frac{1}{x}$ | D． | y=2x |
10．如图是函数f（x）=Acos（ωx+φ）的一段图象，则函数f（x）图象上的最高点坐标为（ ）
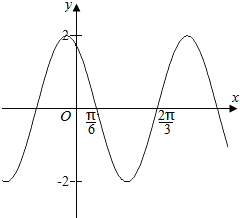
| A． | （$\frac{kπ}{2}$，2），k∈Z | B． | （kπ，2），k∈Z | C． | （2kπ-$\frac{π}{6}$，2），k∈Z | D． | （kπ-$\frac{π}{12}$，2），k∈Z |
4．已知点P为抛物线C：x2=2py（p＞0）上任意一点，O为坐标原点，点M（0，m），若|PM|≥|OM|恒成立，则实数m的取值范围为（ ）
| A． | （-∞，$\frac{p}{4}$] | B． | （-∞，$\frac{p}{2}$] | C． | （-∞，p] | D． | （-∞，2p] |
8．现有五个球分别记为A，B，C，D，E，随机放进三个盒子，每个盒子不空，则A、B在同一盒中的概率是（ ）
| A． | $\frac{6}{25}$ | B． | $\frac{11}{25}$ | C． | $\frac{4}{15}$ | D． | $\frac{6}{15}$ |