题目内容
20.下列四种函数中,表示同一函数的是( )| A. | y=x-1与$y=\sqrt{{{(x-1)}^2}}$ | B. | y=x2与$y={(\sqrt{x})^4}$ | C. | y=4lgx与y=2lgx2 | D. | y=x2与$y=\root{3}{x^6}$ |
分析 分别判断两个函数的定义域和对应法则是否一致,否则不是同一函数.
解答 解:A.$y=\sqrt{{{(x-1)}^2}}$=|x-1|,两个函数的对应法则不同,所以A不是同一函数.
B.$y={(\sqrt{x})^4}$=x2,的定义域为[0,+∞),所以定义域不同,所以B不是同一函数.
C.y=4lgx的定义域为(0,+∞),y=2lgx2,的定义域为{x|x≠0},两个函数的定义域不同,所以C不是同一函数,
D.$y=\root{3}{x^6}$=x2,所以两个函数的定义域和对应法则一致,所以D表示同一函数.
故选:D
点评 本题主要考查判断两个函数是否为同一函数,判断的标准就是判断两个函数的定义域和对应法则是否一致,否则不是同一函数.

练习册系列答案
相关题目
10.样本数据:-2,-1,0,1,2的方差为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | 2.5 |
11.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,若以点F为圆心,半径为a的圆与双曲线C的渐近线相切,则双曲线C的离心率等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
9.下列函数中,在区间(0,1]上是增函数且最大值为-1的为( )
| A. | y=-x2 | B. | $y={(\frac{1}{2})^x}$ | C. | $y=-\frac{1}{x}$ | D. | y=2x |
10.如图是函数f(x)=Acos(ωx+φ)的一段图象,则函数f(x)图象上的最高点坐标为( )
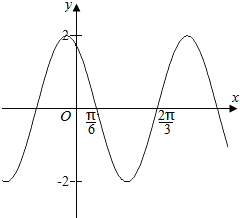

| A. | ($\frac{kπ}{2}$,2),k∈Z | B. | (kπ,2),k∈Z | C. | (2kπ-$\frac{π}{6}$,2),k∈Z | D. | (kπ-$\frac{π}{12}$,2),k∈Z |