题目内容
三个数a=0.312,b=log20.31,c=20.31,之间的大小关系为( )
| A、b<a<c |
| B、a<b<c |
| C、a<c<b |
| D、b<c<a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用指数函数和对数函数的单调性即可得出.
解答:
解:∵0<0.312<0.310=1,log20.31<log21=0,20.31>20=1,
∴b<a<c.
故选A
∴b<a<c.
故选A
点评:熟练掌握指数函数和对数函数的单调性是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
已知0<x<1,则x(3-3x)取最大值时x的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC的三内角的度数成等差数列,则其中间一项的度数是( )
| A、30° | B、60° |
| C、90° | D、120° |
已知命题 p:?x∈R,cosx≤1,则( )
| A、¬p:?x0∈R,cosx0≥1 |
| B、¬p:?x∈R,cosx≥1 |
| C、¬p:?x∈R,cosx>1 |
| D、¬p:?x0∈R,cosx0>1 |
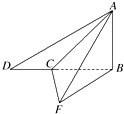 如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(
如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(