题目内容
已知矩阵A对应的变换是先将某平面图形上的点的纵坐标保持不变，横坐标变为原来的2倍，再将所得图形绕原点按顺时针方向旋转90°．
（1）求矩阵A及A的逆矩阵B；
（2）已知矩阵M=
，求M的特征值和特征向量；
（3）若α=
在矩阵B的作用下变换为β，求M50β（运算结果用指数式表示）．
（1）求矩阵A及A的逆矩阵B；
（2）已知矩阵M=
|
（3）若α=
|
考点：矩阵特征值的定义,几种特殊的矩阵变换
专题：选作题,矩阵和变换
分析：（1）利用待定系数法，求矩阵A及A的逆矩阵B；
（2）利用特征多项式，求特征值，进而可求特征向量；
（3）确定β=
-
，再求M50β．
（2）利用特征多项式，求特征值，进而可求特征向量；
（3）确定β=
| 26 |
| 5 |
|
| 7 |
| 5 |
|
解答：
解：（1）矩阵A对应的变换是先将某平面图形上的点的纵坐标保持不变，横坐标变为原来的2倍，为
，
将所得图形绕原点按顺时针方向旋转90°，为A=
．
|A|=2，∴B=
；
（2）特征多项式f（λ）=
，
令f（λ）=0，解得M的特征值λ1=6，λ2=1，
设
是矩阵M属于特征值λ2=1的特征向量，
则
=
，∴
取x=3，得
，
同理矩阵M属于特征值λ2=6的特征向量为
；
（3）β=
-
∴M50β=
．
|
将所得图形绕原点按顺时针方向旋转90°，为A=
|
|A|=2，∴B=
|
（2）特征多项式f（λ）=
|
令f（λ）=0，解得M的特征值λ1=6，λ2=1，
设
|
则
|
|
|
|
取x=3，得
|
同理矩阵M属于特征值λ2=6的特征向量为
|
（3）β=
| 26 |
| 5 |
|
| 7 |
| 5 |
|
∴M50β=
|
点评：本题考查矩阵的性质和应用、特征值与特征向量的计算，解题时要注意特征值与特征向量的计算公式的运用．
练习册系列答案
相关题目
圆x2+2x+y2-4y+3=0与直线x+y+b=0相切，正实数b的值为（ ）
A、
| ||
| B、1 | ||
C、2
| ||
| D、3 |
设n是自然数，f（n）=1+
+
+…+
，经计算可得，f（2）=
，f（4）＞2，f（8）＞
，f（16）＞3，f（32）＞
．观察上述结果，可得出的一般结论是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
A、f（2n）＞
| ||
B、f（n2）≥
| ||
C、f（2n）≥
| ||
D、f(2n)＞
|
设F1，F2是椭圆
+
=1的左、右两个焦点，若椭圆上满足PF1⊥PF2的点P有且只有两个，则离心率e的值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
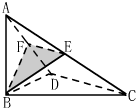如图，△BCD中，∠BCD=90°，AB⊥平面BCD，E，F分别为AC，AD的中点．