题目内容
16.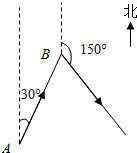 如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?
如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?
分析 设x小时后甲船到达C点,乙船到达D点,则BC=100-50x,BD=30x,由已知可得∠CBD=60°.由余弦定理得CD2=BC2+BD2-2BC•BD•cos∠CBD,即可得出结论.
解答 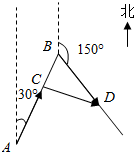 解:如图,设x小时后甲船到达C点,乙船到达D点,
解:如图,设x小时后甲船到达C点,乙船到达D点,
则BC=100-50x,BD=30x,由已知可得∠CBD=60°.
由余弦定理得CD2=BC2+BD2-2BC•BD•cos∠CBD,
即CD2=(100-50x)2+(30x)2-2(100-50x)•30x•cos60°
=100(49x2-130x+100),
当x=$\frac{130}{2×49}$=$\frac{65}{49}$时CD2最小,即CD最小
所以航行$\frac{65}{49}$小时两船之间距离最短.
点评 本题考查利用数学知识解决实际问题,考查余弦定理的运用,考查学生分析解决问题的能力,正确运用余弦定理是关键.

练习册系列答案
相关题目
4.函数f(x)=($\frac{1}{3}$)x在区间[-2,-1]上的最大值是( )
| A. | 1 | B. | 9 | C. | 27 | D. | $\frac{1}{3}$ |
8.为了得到函数$y=\frac{1}{2}sin(2x+\frac{π}{3})$的图象,可以把函数$y=\frac{1}{2}sin2x$的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
5.设α,β是方程x2-2mx+2-m=0(x∈R)的两个实根,则α2+β2的最小值为( )
| A. | 2 | B. | 0 | C. | 16 | D. | -$\frac{17}{4}$ |
6.设函数f(x)=-$\frac{5}{3}$x3+bx-c,其导数为f′(x),若f′(1)=-2,则二项式(bx+$\frac{1}{x}$)5的展开式中x3的系数为( )
| A. | 10250 | B. | 3430 | C. | 825 | D. | 405 |