题目内容

2．已知三棱锥P-ABC中，AB=AC=2，∠BAC=90°，PA⊥平面ABC，且PA=2，求这个三棱锥的外接球的半径．

分析 将三棱锥补成长方体，它的对角线是其外接球的直径，从而即可求得这个三棱锥的外接球的半径．

解答 解：由PA⊥平面ABC，AB⊥AC，将三棱锥补成长方体，它的对角线是其外接球的直径，则
三棱锥外接球的直径为2$\sqrt{3}$，半径为$\sqrt{3}$．

点评 本题考查这个三棱锥的外接球的半径，考查学生分析解决问题的能力，得出将三棱锥补成长方体，它的对角线是其外接球的直径是解题的关键．

练习册系列答案
相关题目
12．已知x∈[-$\frac{π}{4}$，$\frac{π}{3}$]，函数y=tan2x-tan（π-x）+1的值域是[$\frac{3}{4}$，4+$\sqrt{3}$]．
13．若直线的倾斜角为α，则直线的斜率为tanα或不存在．
10．经过点P（-3，-5），且倾斜角为90°的直线方程是x=-3．
17．已知定义在R上的奇函数f（x），其导函数为f′（x），对任意正实数x满足xf′（x）＞2f（-x），若g（x）=x2f（x），则不等式g（x）＜g（1-3x）的解集是（　　）
A．（$\frac{1}{4}$，+∞）B．（-∞，$\frac{1}{4}$）C．（0，$\frac{1}{4}$）D．（-∞，$\frac{1}{4}$）∪（$\frac{1}{4}$，+∞）
7．已知f（x-1）=x2+2x-4，则f（-3）=-4．
14．已知tanα=$\frac{3}{4}$，α∈（$\frac{π}{2}$，$\frac{3π}{2}$），求：
（1）$\frac{sin（π+α）-sin（\frac{3π}{2}+α）}{cos（3π-α）+2}$；
（2）cos（-π-α）
15．与圆C：（x-2）2+（y+1）2=4相切于点（4，-1）且半径为1的圆的方程是（x-5）2+（y+1）2=1或或（x-3）2+（y+1）2=1．
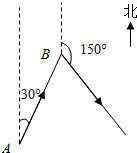16．如图所示，已知A、B两点的距离为100海里，B在A的北偏东30°处，甲船自A以50海里/小时的速度向B航行，同时乙船自B以30海里/小时的速度沿方位角150°方向航行．问航行几小时两船之间的距离最短？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网