题目内容
15.已知函数f(x)=x2-ax+lnx(a∈R).(1)若函数f(x)在x=1处取得极小值,求函数f(x)的极大值;
(2)若x∈(0,e]时,函数f(x)≤1恒成立,求a的取值范围.
分析 (1)由f(x)=x2-ax+lnx(a∈R)在x=1时取得极值,可得f′(1)=0,解出a即可得出.
(2)x∈(0,e]时,函数f(x)≤1恒成立,可得a≥x+$\frac{lnx}{x}$-$\frac{1}{x}$=h(x).利用导数研究其单调性极值与最值即可得出.
解答 解:(1)∵f(x)=x2-ax+lnx(a∈R)在x=1时取得极值,f′(x)=2x-a+$\frac{1}{x}$,
∴f′(1)=0,
∴2-a+1=0,
解得a=3,经过验证满足条件.
(2)∵x∈(0,e]时,函数f(x)≤1恒成立,∴a≥x+$\frac{lnx}{x}$-$\frac{1}{x}$=h(x).
h′(x)=1+$\frac{1}{{x}^{2}}$+$\frac{1-lnx}{{x}^{2}}$=$\frac{{x}^{2}+2-lnx}{{x}^{2}}$>0,
∴函数h(x)在x∈(0,e]单调递增,
∴x=e时,h(x)取得最大值,h(e)=e+$\frac{1}{e}$-$\frac{1}{e}$=e.
∴a≥e.
点评 本题考查了利用导数研究函数的极值与最值,考查了等价转化方法、推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知函数f(x)=lnx-($\frac{1}{2}$)x+1,则不等式f(2x-3)<$\frac{1}{2}$的解集为( )
| A. | {x|{$\frac{3}{2}$<x<2} | B. | {x|${\frac{1}{2}$<x<2} | C. | {x|x<1} | D. | {x|-1<x<$\frac{3}{2}}\right.$} |
7.已知函数y=f(x)的图象关于原点对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立,若a=(-2)×f(-2),b=f(1),c=3×f(3),则a,b,c的关系大小是( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
5.过点(2,0)引直线l与曲线$y=\sqrt{2-{x^2}}$相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\sqrt{3}$ | C. | $±\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
 在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.
在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.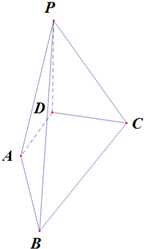 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.