题目内容
19.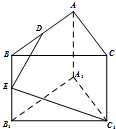 在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )
在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
分析 设侧棱AA1的长为2x,则由题意,可得4+x2+1+x2=4x2+(2×$\frac{\sqrt{3}}{2}$ )2,求出x,即可得出结论
解答 解:取A1B1的中点D1,
连接DD1,C1D1,DC1,
设侧棱AA1的长为2x,
则由题意,可得4+x2+1+x2=4x2+(2×$\frac{\sqrt{3}}{2}$ )2,
∴x=1,2x=2.
故选:B.
点评 本题考查侧棱AA1的长的计算,考查勾股定理的运用,正确运用勾股定理是关键.

练习册系列答案
相关题目
7.已知函数y=f(x)的图象关于原点对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立,若a=(-2)×f(-2),b=f(1),c=3×f(3),则a,b,c的关系大小是( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
8.一个多面体的三视图如图所示,则此多面体的表面积是( )


| A. | 10 | B. | 12 | C. | 8+4$\sqrt{2}$ | D. | 12+4$\sqrt{2}$ |
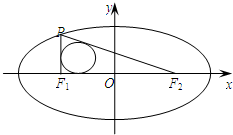 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0. 在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.
在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.