题目内容
15.抛物线x2=-4y的焦点到准线的距离为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意,由抛物线的标准方程计算可得抛物线的焦点坐标和准线方程,计算即可得答案.
解答 解:根据题意,抛物线的方程为x2=-4y,
其焦点坐标为(0,-1),准线方程为y=1,
焦点到准线的距离为2;
故选:B.
点评 本题考查抛物线的标准方程,关键是掌握抛物线的标准方程.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
6.一元二次不等式-x2+x+2>0的解集是( )
| A. | {x|x<-1或x>2} | B. | {x|x<-2或x>1} | C. | {x|-1<x<2} | D. | {x|-2<x<1} |
3.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=x3+x | B. | y=-$\frac{1}{x}$ | C. | y=sinx | D. | $y={({\frac{1}{2}})^x}-{2^x}$ |
20.不等式x2-3x-10>0的解集是( )
| A. | {x|-2≤x≤5} | B. | {x|x≥5或x≤-2} | C. | {x|-2<x<5} | D. | {x|x>5或x<-2} |
5.函数y=$\frac{1}{2}sin2x+{sin^2}$x,x∈R的递减区间为( )
| A. | $[{kπ-\frac{π}{8},kπ+\frac{π}{8}}],k∈Z$ | B. | $[{\frac{kπ}{2}-\frac{π}{8},\frac{kπ}{2}+\frac{π}{8}}],k∈Z$ | ||
| C. | $[{kπ+\frac{3π}{8},kπ+\frac{7π}{8}}],k∈Z$ | D. | $[{\frac{kπ}{2}+\frac{3π}{8},\frac{kπ}{2}+\frac{7π}{8}}],k∈Z$ |
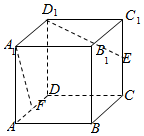 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是CC1,AD的中点,那么异面直线D1E和A1F所成角的余弦值等于$\frac{2}{5}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是CC1,AD的中点,那么异面直线D1E和A1F所成角的余弦值等于$\frac{2}{5}$.