题目内容
8．若集合A={x|x2＜4}，且A∪B=A，则集合B可能是（ ）| A． | {1，2} | B． | {x|x＜2} | C． | {-1，0，1} | D． | R |
分析 化简集合A，根据A∪B=A，即可判断集合B．
解答 解：集合A={x|x2＜4}={x|-2＜x＜2}．
∵A∪B=A，
∴B⊆A．
∵{-1，0，1}⊆A，
故选C．
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
相关题目
16．
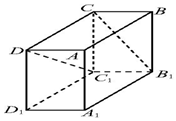在长方体ABCD-A1B1C1D1中，B1C和C1D与底面所成的角分别为60°和45°，则异面直线B1C和C1D所成角的余弦值为（ ）
在长方体ABCD-A1B1C1D1中，B1C和C1D与底面所成的角分别为60°和45°，则异面直线B1C和C1D所成角的余弦值为（ ）| A． | $\frac{{\sqrt{6}}}{4}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{2}}}{6}$ | D． | $\frac{{\sqrt{2}}}{3}$ |
3．定义在R上的偶函数f（x）满足：对任意的x1，x2∈[0，+∞）（x1≠x2），有$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}＜0$．则（ ）
| A． | f（3）＜f（-2）＜f（1） | B． | f（1）＜f（-2）＜f（3） | C． | f（-2）＜f（1）＜f（3） | D． | f（3）＜f（1）＜f（-2） |
13．以F（0，1）为焦点的抛物线的标准方程是（ ）
| A． | x2=4y | B． | x2=2y | C． | y2=4x | D． | y2=2x |
17．设函数f（x）是定义在R上的函数，满足f（x）=f（4-x），且对任意x1，x2∈（0，+∞），都有（x1-x2）[f（x1+2）-f（x2+2）]＞0，则满足f（2-x）=f（$\frac{3x+11}{x+4}$）的所有x的和为（ ）
| A． | -3 | B． | -5 | C． | -8 | D． | 8 |
18．一个棱长为6的正四面体纸盒内放一个正方体，若正方体可以在纸盒内任意转动，则正方体棱长的最大值为（ ）
| A． | 3 | B． | 2 | C． | $\sqrt{2}$ | D． | 1 |