题目内容
6.函数f(x)的定义域为R,周期为1,当0≤x<1时f(x)=x,若函数f(x)的图象与$g(x)=2{x^2}+\sqrt{k}$的图象只有一个交点,则实数k的取值范围是( )| A. | $[\frac{1}{64},1]$ | B. | $[\frac{1}{8},1]$ | C. | $(\frac{1}{64},1)$ | D. | $(\frac{1}{8},1)$ |
分析 画出函数的图象,利用函数f(x)的图象与$g(x)=2{x^2}+\sqrt{k}$的图象只有一个交点,列出方程转化求解即可.
解答 解:函数f(x)的定义域为R,周期为1,当0≤x<1时f(x)=x,函数f(x)的图象与$g(x)=2{x^2}+\sqrt{k}$的图象,如图,y=f(x)的图象与y=g(x)的图象只有一个交点,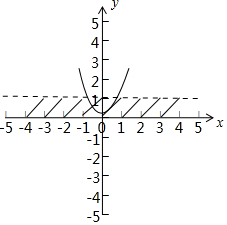
可知2x2+$\sqrt{k}$=x只有一个公共点,可得△=1-8$\sqrt{k}$=0,解得k=$\frac{1}{64}$,
此时,直线y=x(x∈(0,1))与y=2x2+$\sqrt{k}$相切,有两个交点,
其中函数y=2x2+$\sqrt{k}$在(-1,0),只有一个交点,
当x=-1时,g(-1)=2+$\frac{1}{8}$>1,说明x<-1没有公共点,当k>1时,g(0)=$\sqrt{k}$>1没有公共点.
函数f(x)的图象与$g(x)=2{x^2}+\sqrt{k}$的图象只有一个交点,结合图象可得k$∈(\frac{1}{64},1)$.
故选:C.
点评 本题考查函数的图象的应用,函数的零点与方程根的关系,考查转化思想以及计算能力.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
16.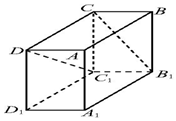 在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
 在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
17.设函数f(x)是定义在R上的函数,满足f(x)=f(4-x),且对任意x1,x2∈(0,+∞),都有(x1-x2)[f(x1+2)-f(x2+2)]>0,则满足f(2-x)=f($\frac{3x+11}{x+4}$)的所有x的和为( )
| A. | -3 | B. | -5 | C. | -8 | D. | 8 |
1.已知一个圆锥的正视图和侧视图都是边长为1的正三角形,则它的俯视图的面积是( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
11. 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( )| A. | 210-1 | B. | 210 | C. | 310-1 | D. | 310 |
18.一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
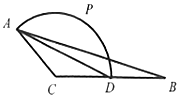 已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.
已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.