题目内容
13.i是虚数单位,若实数x,y满足(1+i)x+(1-i)y=2,复数z=$\frac{x+i}{y-i}$(i是虚数单位),$\overline{z}$是z的共轭复数,则z•$\overline{z}$=( )| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
分析 利用复数相等,求出x,y,然后利用复数的除法化简z,即可求解z•$\overline{z}$.
解答 解:实数x,y满足(1+i)x+(1-i)y=2,
可得$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$,解得x=y=1,
复数z=$\frac{x+i}{y-i}$=$\frac{1+i}{1-i}$=$\frac{(1+i)(1+i)}{(1-i)(1+i)}$=i.
则z•$\overline{z}$=i•(-i)=1.
故选:A.
点评 本题考查复数的基本运算,复数相等以及复数的基本概念的应用,考查计算能力.

练习册系列答案
相关题目
2.为分析学生初中升学的数学成绩对高一数学学习的影响,在高一年级随机抽取10名学生,了解他们的人学数学成绩和高一期末考试数学成绩如下表:
(1)画出散点图;
(2)对变量x与y进行相关性检验,如果x与y之间具有线性相关关系,求出回归直线方程.
(3)若某学生人学的数学成绩为80分,试估计他在高一期末考试中的数学成绩.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 入学成绩(x/分) | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
| 高一期末成绩(y/分) | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(2)对变量x与y进行相关性检验,如果x与y之间具有线性相关关系,求出回归直线方程.
(3)若某学生人学的数学成绩为80分,试估计他在高一期末考试中的数学成绩.
16.为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚,为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
若用表中数据所得频率代替概率.
(Ⅰ)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民分为两类:A类市民在罚金不超过10元时就会改正行为;B类是其他市民,现对A类和B类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为B类市民的概率是多少?
| 处罚金额x(单位:元) | 5 | 10 | 15 | 20 |
| 会闯红灯的人数y | 50 | 40 | 20 | 10 |
(Ⅰ)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民分为两类:A类市民在罚金不超过10元时就会改正行为;B类是其他市民,现对A类和B类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为B类市民的概率是多少?
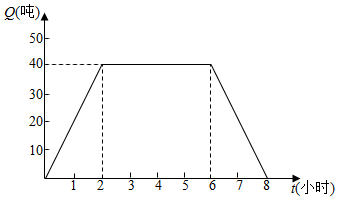 某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.
某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.