题目内容
8. 某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.
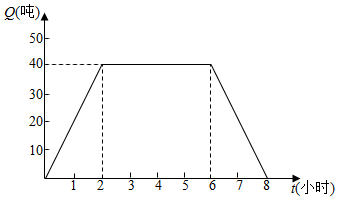
某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.
分析 根据条件利用待定系数法进行求解即可.
解答 解:当0≤t≤2时,函数为过原点的直线,设Q=kt,
当t=2时,Q=40,此时2k=40,则k=20,此时函数的解析式为Q=20t,
当2≤t≤5时,函数为常数,此时Q=40,
当5≤t≤8时,设直线方程为Q=at+b,
此时直线过(8,0),(5,40),
则$\left\{\begin{array}{l}{8a+b=0}\\{5a+b=40}\end{array}\right.$得a=-$\frac{40}{3}$,b=$\frac{320}{3}$,此时Q=-$\frac{40}{3}$t+$\frac{320}{3}$,
则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$,
故答案为:Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$
点评 本题主要考查函数解析式的求解,根据图象利用待定系数法结合直线方程的求法是解决本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.已知命题p:?x∈R,x2-2x+4≤0,则?p为( )
| A. | ?x∈R,x2-2x+4≥0 | B. | $?{x_0}∈R,x_0^2-2{x_0}+4>0$ | ||
| C. | ?x∉R,x2-2x+4≤0 | D. | $?{x_0}∉R,x_0^2-2{x_0}+4>0$ |
19.在半径不等的两个圆内,1rad的圆心角( )
| A. | 所对的弧长相等 | B. | 所对的弦长相等 | ||
| C. | 所对的弧长等于各自的半径 | D. | 所对的弧长为$\frac{57.3°}{180°}$R |
13.i是虚数单位,若实数x,y满足(1+i)x+(1-i)y=2,复数z=$\frac{x+i}{y-i}$(i是虚数单位),$\overline{z}$是z的共轭复数,则z•$\overline{z}$=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
11.已知定义在R上的函数f(x)满足:f(x+y)=f(x)+f(y)+1,若f(8)=15,则f(2)=( )
| A. | $\frac{15}{4}$ | B. | 3 | C. | 2 | D. | -1 |
 如图,已知抛物线y=ax2+bx+c(a≠0)的图象过原点,并交x轴于A(-6,0),抛物线的顶点B的纵坐标为-$\sqrt{3}$.
如图,已知抛物线y=ax2+bx+c(a≠0)的图象过原点,并交x轴于A(-6,0),抛物线的顶点B的纵坐标为-$\sqrt{3}$.