题目内容
设A为不等式组表示的平面区域
,则当a从-1连续变化到0时,动直线x-y=a扫过A中的那部分区域的面积为 .
|
考点:简单线性规划的应用
专题:数形结合,不等式的解法及应用
分析:先由不等式组画出其表示的平面区域,再确定动直线x-y=a的变化范围,最后由三角形面积公式解之即可.
解答:
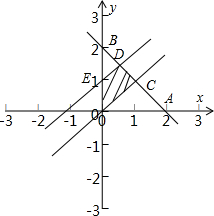 解:如图,不等式组
解:如图,不等式组
表示的平面区域是△AOB,
动直线x-y=a(即y=x-a)在y轴上的截距从0变化到1.
知△OBC是斜边为2的等腰直角三角形,△BDE是直角边为1等腰直角三角形,
所以区域的面积S阴影=S△OBC-S△BDE=
×2×1-
×1×
=
.
故答案为:
.
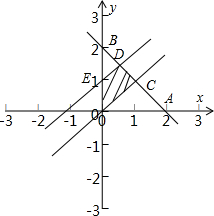 解:如图,不等式组
解:如图,不等式组
|
动直线x-y=a(即y=x-a)在y轴上的截距从0变化到1.
知△OBC是斜边为2的等腰直角三角形,△BDE是直角边为1等腰直角三角形,
所以区域的面积S阴影=S△OBC-S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
如果命题p:|x-1|+|y-2|=0,命题q:(x-1)(y-2)=0,那么命题p是命题q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |