题目内容
14.A,B,C是圆O上不同的三点,线段CO与线段AB交于点D,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(λ∈R,μ∈R),则λ+μ的取值范围是( )| A. | (1,+∞) | B. | (0,1) | C. | (1,$\sqrt{2}$] | D. | (-1,0) |
分析 可作图:取∠AOB=120°,∠AOC=∠BOC=60°,从而便得到四边形AOBC为菱形,这样便有$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$,从而根据平面向量基本定理即可得到λ+μ=2,这样便可排除选项B,C,D,从而便可得出正确选项.
解答 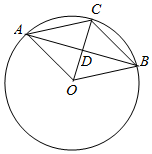 解:∵A,B,C是圆0上不同的三点,线段C0与线段AB交于点D;
解:∵A,B,C是圆0上不同的三点,线段C0与线段AB交于点D;
∴如图所示,不妨取∠AOB=120°,∠AOC=∠BOC=60°,则四边形AOBC为菱形;
∴$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$;
又$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$;
∴λ=μ=1,λ+μ=2,∴可排除B,C,D选项.
故选:A.
点评 考查排除的方法做选择题,菱形的概念,等边三角形的概念,以及向量加法的平行四边形法则,平面向量基本定理.

练习册系列答案
相关题目
5.已知曲线y=x-1与直线x=1,x=3,x轴围成的封闭区域为A,直线x=1,x=3,y=0,y=1围成的封闭区域为B,在区域B内任取一点P,该点P落在区域A的概率为$\frac{ln3}{2}$.
2.已知点F(-c,0)(c>0)是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左焦点,过F作直线与圆x2+y2=a2相切,并与渐近线交于第一象限内一点P,满足|$\overrightarrow{OF}$|=|$\overrightarrow{OP}$|,则该双曲线的离心率等于( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |



