题目内容
3.已知f(x)为偶函数,当x<0时,f(x)=ln(-x)+3x,则曲线y=f(x)在点(1,f(1))处的切线方程是2x+y+1=0.分析 由偶函数的定义,可得f(-x)=f(x),即有x>0时,f(x)=lnx-3x,求出导数,求得切线的斜率,由点斜式方程可得切线的方程.
解答 解:f(x)为偶函数,可得f(-x)=f(x),
当x<0时,f(x)=ln(-x)+3x,即有
x>0时,f(x)=lnx-3x,
f′(x)=$\frac{1}{x}$-3,
可得f(1)=ln1-3=-3,f′(1)=1-3=-2,
则曲线y=f(x)在点(1,-3)处的切线方程为y-(-3)=-2(x-1),
即为2x+y+1=0.
故答案为:2x+y+1=0.
点评 本题考查导数的运用:求切线的方程,同时考查函数的奇偶性的定义和运用,考查运算能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
11.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,点M,N为长轴的两个端点,若在椭圆上存在点H,使${k_{MH}}{k_{NH}}∈(-\frac{1}{2},0)$,则离心率e的取值范围为( )
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
8.已知函数f(x)=|x-a|
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若存在实数x,使不等式f(x)+f(x+5)<m成立,求实数m的取值范围.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若存在实数x,使不等式f(x)+f(x+5)<m成立,求实数m的取值范围.
13.已知圆C的方程为x2+y2=1,直线l的方程为x+y=2,过圆C上任意一点P作与l夹角为45°的直线交l于A,则|PA|的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{2}$ |

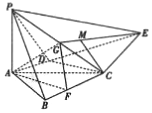 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.