题目内容

17．集合A={x|ax-1=0}，B={x|x2-x-6-0}，若A?B，求实数a的值．

分析 先化简集合B={3，-2}，集合A中至多有一个元素，分类对其求解即可，本题要分成两类，一类为无解，一类为有一解．

解答 解：集合B={3，-2}，集合A中至多有一个元素，
 若集合A空集，即a=0时，显然满足A?B，故a=0．
 若集合A非空集，即a≠0，此时A={-$\frac{1}{a}$}，若-$\frac{1}{a}$=3，则a=-$\frac{1}{3}$，若-$\frac{1}{a}$=-2，则a=$\frac{1}{2}$
故a的取值集合为{0，-$\frac{1}{3}$，$\frac{1}{2}$}．

点评 本题的考点是集合的包含关系判断及应用，本题考查利用集合的包含关系求参数，此类题一般要进行分类讨论求参数的值，求解本题时不要忘记集合为空集的情况，此为本题的易错点．

练习册系列答案
相关题目
14．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率e=$\frac{{\sqrt{2}}}{2}$，左顶点为A（-2，0）．
（1）求椭圆E的方程；
（2）已知O为坐标原点，B，C是椭圆E上的两点，连接AB的直线平行OC交y轴于点D，证明：|AB|$，\;\;\sqrt{2}|{OC}|\;\;，\;\;|{AD}$|成等比数列．
15．已知m，n是两条不同的直线，α，β是两个不重合的平面．命题p：若α∩β=m，m⊥n，则n⊥α；命题q：若m∥α，m?β，α∩β=n，则m∥n．那么下列命题中的真命题是（　　）
A．p∧qB．p∨￢qC．￢p∧qD．￢p∧￢q
5．记关于x的不等式$1-\frac{a}{x}＜0$的解集为P，不等式|x+2|＜3的解集为Q
（1）若a=3，求P；
（2）若P∪Q=Q，求正数a的取值范围．
12．已知p是一个素数，n和α都是正整数，且满足3n-2n=pα．求证：n是一个素数．
2．若直线l过三角形ABC内心（三角形内心为三角形内切圆的圆心），则“直线l平分三角形ABC周长”是“直线l平分三角形ABC面积”的（　　）条件．
A．充分不必要B．必要不充分
C．充要D．既不充要也不必要
9．如图，在△AOC中，∠O=90°，∠C=30°，B是边OA上一点，D是边OC上一动点，且当CD=100（$\sqrt{3}$-1）时，∠ADO=45°
（1）求OA的长；
（2）当AB=52，tan∠ADB=$\frac{13\sqrt{3}}{60}$时，求CD的长．
6．下列命题中为真命题的是③④．
①若两个平面α∥β，a?α，b?β，则a∥b；
②若两个平面α∥β，a?α，b?β，则a与b一定异面；
③若两个平面α∥β，a?α，b?β，则a与b一定不相交；
④若两个平面α∥β，a?α，b?β，则a与b共面或异面；
⑤若两个平面α∥β，a?α，则a与β一定相交．
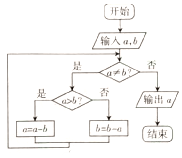7．秦九韶是我国南宋时期的数学家，他所著的《九章算术》是我国古代数学名著，体现了我国古代数学的辉煌成就．其中的“更相减损术”蕴含了丰富的思想，根据“更相减损术”的思想设计了如图所示的程序框图，若输入的a=15，输出的a=3，则输入的b可能的值为（　　）
A．30B．18C．5D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网