题目内容
6.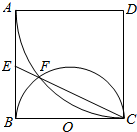 如图,正方形ABCD中,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接CF并延长交AB于点E.
如图,正方形ABCD中,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接CF并延长交AB于点E.(Ⅰ)求证:AE=EB;
(Ⅱ)若EF•FC=$\frac{4}{5}$,求正方形ABCD的面积.
分析 (Ⅰ)推导出EA为圆D的切线,且EB是圆O的切线,由此利用切割线定理能证明AE=EB.
(Ⅱ)设正方形的边长为a,连结BF,由射影定理能求出正方形ABCD的面积.
解答  证明:(Ⅰ)∵以D为圆心、DA为半径的圆弧与以BC为直径半圆交于点F,
证明:(Ⅰ)∵以D为圆心、DA为半径的圆弧与以BC为直径半圆交于点F,
且四边形ABCD为正方形,
∴EA为圆D的切线,且EB是圆O的切线,
由切割线定理得EA2=EF•EC,
故AE=EB.
(Ⅱ)设正方形的边长为a,连结BF,
∵BC为圆O的直径,∴BF⊥EC,
在Rt△BCE中,由射影定理得EF•FC=BF2=$\frac{4}{5}$,
∴BF=$\frac{2}{5}\sqrt{5}$=$\frac{a×\frac{a}{2}}{\sqrt{{a}^{2}+(\frac{a}{2})^{2}}}$,解得a=2,
∴正方形ABCD的面积为4.
点评 本题考查两线段相等的证明,考查正方形面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
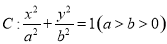 过点
过点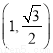 ,且离心率为
,且离心率为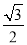 .
.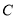 的标准方程;
的标准方程;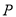 与点
与点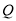 均在椭圆
均在椭圆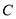 上,且
上,且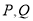 关于原点对称,问:椭圆上是否存在点
关于原点对称,问:椭圆上是否存在点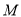 (点
(点 在一象限),使得
在一象限),使得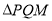 为等边三角形?若存在,求出点
为等边三角形?若存在,求出点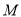 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.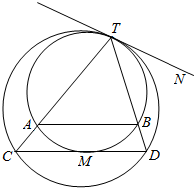 如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.
如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M. 分别是
分别是 内角
内角 的对边,
的对边, .
. ,求
,求 ;
; ,且
,且 ,求
,求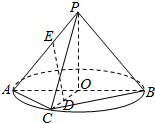 如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.
如图,圆锥的轴截面PAB是等腰直角三角形,AB的中点为O,C是底面圆周上异于A,B的任意一点,D为线段OC的中点,E为母线PA上一点,且AE=3EP.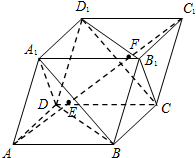 如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$.
如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$. 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=$\frac{π}{2}$,E、F依次为CC1和BC的中点:
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=$\frac{π}{2}$,E、F依次为CC1和BC的中点: