题目内容
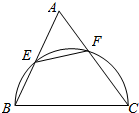
15.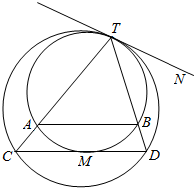 如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.
如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.(Ⅰ)证明:AB∥CD;
(Ⅱ)证明:AC•MD=BD•CM.
分析 (Ⅰ)证明∠TCD=∠TAB,即可证明AB∥CD;
(Ⅱ)证明:∠MTD=∠ATM,利用正弦定理证明$\frac{MD}{MC}=\frac{TD}{TC}$,由AB∥CD知$\frac{TD}{TC}=\frac{BD}{AC}$,即可证明AC•MD=BD•CM.
解答 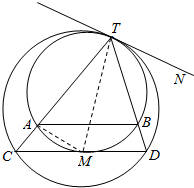 (Ⅰ)由弦切角定理可知,∠NTB=∠TAB,…(3分)
(Ⅰ)由弦切角定理可知,∠NTB=∠TAB,…(3分)
同理,∠NTB=∠TCD,所以,∠TCD=∠TAB,
所以,AB∥CD.…(5分)
(Ⅱ)连接TM、AM,
因为CD是切内圆于点M,
所以由弦切角定理知,∠CMA=∠ATM,
又由(Ⅰ)知AB∥CD,
所以,∠CMA=∠MAB,又∠MTD=∠MAB,
所以∠MTD=∠ATM.…(8分)
在△MTD中,由正弦定理知,$\frac{MD}{sin∠DTM}=\frac{TD}{sin∠TMD}$,
在△MTC中,由正弦定理知,$\frac{MC}{sin∠ATM}=\frac{TC}{sin∠TMC}$,因∠TMC=π-∠TMD,
所以$\frac{MD}{MC}=\frac{TD}{TC}$,由AB∥CD知$\frac{TD}{TC}=\frac{BD}{AC}$,
所以$\frac{MD}{MC}=\frac{BD}{AC}$,即,AC•MD=BD•CM.…(10分)
点评 本题考查正弦定理,弦切角定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
5. 2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
注:(1)表中a/b表示出手b次命中a次;
(2)TS%(真实得分率)是衡量球员进攻的效率,其计算公式为:
TS%=$\frac{全场得分}{2×(投篮出手次数+0.44×罚球出手次数)}$.
(Ⅰ)求表中x的值;
(Ⅱ)从上述9场比赛中随机选择一场,求易建联在该场比赛中TS%超过50%的概率;
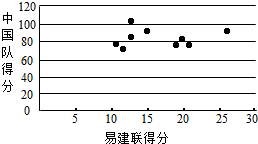
(Ⅲ)用x来表示易建联某场的得分,用y来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断y与x之间是否具有线性相关关系?结合实际简单说明理由.
 2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.| 比分 | 易建联技术统计 | |||
| 投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
| 中国91-42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
| 中国76-73韩国 | 7/13 | 6/8 | 20 | 60.53% |
| 中国84-67约旦 | 12/20 | 2/5 | 26 | x |
| 中国75-62哈萨克期坦 | 5/7 | 5/5 | 15 | 81.52% |
| 中国90-72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
| 中国85-69卡塔尔 | 4/10 | 4/4 | 13 | 55.27% |
| 中国104-58印度 | 8/12 | 5/5 | 21 | 73.94% |
| 中国70-57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
| 中国78-67菲律宾 | 4/14 | 3/6 | 11 | 33.05% |
(2)TS%(真实得分率)是衡量球员进攻的效率,其计算公式为:
TS%=$\frac{全场得分}{2×(投篮出手次数+0.44×罚球出手次数)}$.
(Ⅰ)求表中x的值;
(Ⅱ)从上述9场比赛中随机选择一场,求易建联在该场比赛中TS%超过50%的概率;
(Ⅲ)用x来表示易建联某场的得分,用y来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断y与x之间是否具有线性相关关系?结合实际简单说明理由.
2.焦距为6,离心率e=$\frac{3}{5}$,焦点在y轴上的椭圆标准方程是( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 |
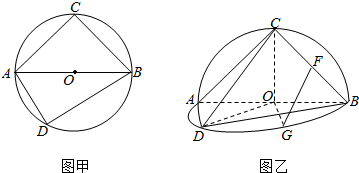
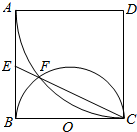 如图,正方形ABCD中,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接CF并延长交AB于点E.
如图,正方形ABCD中,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接CF并延长交AB于点E.