题目内容
19.求与双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1有公共焦点,且过点(3$\sqrt{2}$,2)的双曲线的标准方程.分析 求得双曲线的焦点,可设所求双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),由题意可得c=2$\sqrt{5}$,即a2+b2=20,将点(3$\sqrt{2}$,2)代入双曲线方程,解方程可得a,b,进而得到双曲线的方程.
解答 解:双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1的焦点为(±2$\sqrt{5}$,0),
可设所求双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
由题意可得c=2$\sqrt{5}$,即a2+b2=20,
将点(3$\sqrt{2}$,2)代入双曲线方程可得,
$\frac{18}{{a}^{2}}$-$\frac{4}{{b}^{2}}$=1,
解得a=2$\sqrt{3}$,b=2$\sqrt{2}$,
即有所求双曲线的方程为$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{8}$=1.
点评 本题考查双曲线的方程的求法,注意运用待定系数法,点满足方程,考查运算能力,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
9.若复数$z=\frac{2i}{1-i}$(i是虚数单位),则$\overline z$=( )
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
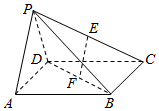 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.
 一个空间几何体的三视图如图所示,则该几何体的体积为8,其外接球的表面积为29π.
一个空间几何体的三视图如图所示,则该几何体的体积为8,其外接球的表面积为29π.