题目内容
14.已知实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{x+y≤2}\\{2x-y-3≤0}\end{array}\right.$,则目标函数z=$\frac{y}{x}$的最大值为1.分析 画出满足条件的平面区域,求出角点的坐标,结合z=$\frac{y}{x}$的几何意义求出z的最大值即可.
解答  解:画出满足条件的平面区域,如图示:
解:画出满足条件的平面区域,如图示:
由$\left\{\begin{array}{l}{x=1}\\{x+y=2}\end{array}\right.$,解得:A(1,1),
∴z=$\frac{y}{x}$的最大值是1,
故答案为:1.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知i是虚数单位,若1+i=z(1-i),则z=( )
| A. | -1 | B. | 1 | C. | -i | D. | i |
6.已知函数f(x)=sin($\frac{x}{2}$+$\frac{π}{4}$),则f($\frac{π}{2}$)=( )
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
3.偶函数f(x)定义在(-1,0)∪(0,1)上,且$f(\frac{1}{2})=0$,当x>0时,总有$(\frac{1}{x}-x)f'(x)•ln(1-{x^2})>2f(x)$,则不等式f(x)<0的解集为( )
| A. | {x|-1<x<1且x≠0} | B. | $\left\{x\right.|-1<x<-\frac{1}{2}$或$\frac{1}{2}<x<\left.1\right\}$ | ||
| C. | $\left\{{x|-\frac{1}{2}}\right.<x<\frac{1}{2}$且x≠0} | D. | {x|-1<x<-$\frac{1}{2}$或$0<x<\left.{\frac{1}{2}}\right\}$ |
4.已知集合A={x|x2-5x-6<0},B={x|-3<x<3},则A∩B=( )
| A. | (-3,3) | B. | (-3,6) | C. | (-1,3) | D. | (-3,1) |
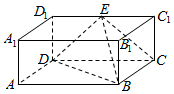 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E为C1D1的中点.