题目内容
已知O是坐标原点，点A（-2，1），若点M（x，y）为平面区域
上的一个动点，则
•
的取值范围是（ ）
|
| OA |
| OM |
| A、[-1，0] |
| B、[-1，2] |
| C、[0，1] |
| D、[0，2] |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，设z=
•
，求出z的表达式，利用z的几何意义，利用数形结合即可得到结论．
| OA |
| OM |
解答：
解：作出不等式组对应的平面区域如图：
z=
•
，
∵A（-2，1），M（x，y），
∴z=
•
=-2x+y，
即y=2x+z，
平移直线y=2x+z，由图象可知当y=2x+z，经过点A（1，1）时，直线截距最小，此时z最小为z=-2+1=-1．
经过点B（0，2）时，直线截距最大，此时z最大．此时z=2，
即-1≤z≤2，
故选：B．
z=
| OA |
| OM |
∵A（-2，1），M（x，y），
∴z=
| OA |
| OM |
即y=2x+z，
平移直线y=2x+z，由图象可知当y=2x+z，经过点A（1，1）时，直线截距最小，此时z最小为z=-2+1=-1．
经过点B（0，2）时，直线截距最大，此时z最大．此时z=2，
即-1≤z≤2，
故选：B．
点评：本题主要考查线性规划的应用，根据向量数量积的坐标公式求出z的表达式，利用数形结合是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知O为坐标原点，P1、P2是双曲线
-
=1上的点．P是线段P1P2的中点，直线OP、P1P2的斜率分别为k1、k2，则k1k2=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合An={x|（x-1）（x-n2-4+lnn）＜0}，当n取遍区间（1，3）内的一切实数，所有的集合An的并集是（ ）
| A、（1，13-ln3） |
| B、（1，6） |
| C、（1，+∞） |
| D、（1，2） |
半径为1的球的内接正三棱柱（底面是正三角形的直棱柱）的侧面积为3
，则正三棱柱的高为（ ）
| 3 |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
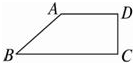一个水平放置的平面图形的斜二测直观图是直角梯形（如图）．∠ABC=45°，AB=AD=1，DC⊥BC，则这个平面图形的面积为（ ） A、
| ||||||
B、2+
| ||||||
C、
| ||||||
D、
|
如图，正方形ABCD的边长为1，延长BA至E，使AE=1，连接EC、ED，则cos2∠CED=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|