题目内容
9.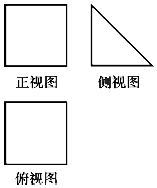 一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )
一块硬质材料的三视图如图所示,正视图和俯视图都是边长为10cm的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
分析 由题意,该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r.
解答 解:由题意,该几何体为三棱柱,所以最大球的半径为正视图直角三角形内切圆的半径r,
则10-r+10-r=10$\sqrt{2}$cm,
∴r=10-5$\sqrt{2}$≈3cm.
故选:A.
点评 本题考查三视图,考查几何体的内切圆,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
20.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,O为坐标原点,M为长轴的一个端点,若在椭圆上存在点N,使ON⊥MN,则离心率e的取值范围为( )
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
4. 下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
 下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )| A. | 230.5,220 | B. | 231.5,232 | C. | 231,231 | D. | 232,231 |
18.执行如图所示的程序框图,若输入p=2017,则输出i的值为( )


| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
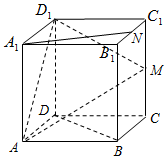 如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点,
如图边长为2的正方体ABCD-A1B1C1D1中,M,N分别是CC1,B1C1的中点, 工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.
工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.