题目内容
双曲线x2-y2=1的顶点到其渐近线的距离等于( )
(A)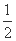 (B)
(B)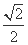 (C)1 (D)
(C)1 (D)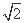
B

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
题目内容
双曲线x2-y2=1的顶点到其渐近线的距离等于( )
(A)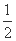 (B)
(B)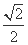 (C)1 (D)
(C)1 (D)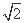
B

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案