题目内容
2.设随机向量η服从正态分布N(1,σ2),若P(η<-1)=0.2,则函数f(x)=$\frac{1}{3}{x^3}+{x^2}+{η^2}$x没有极值点的概率是0.7.分析 令f′(x)=0至多只有1解得出η的范围,再利用正态分布的对称性得出f(x)无极值点的概率.
解答 解:f′(x)=x2+2x+η2,
若f(x)没有极值点,则f′(x)=0最多只有1个解,
∴△=4-4η2≤0,
解得η≤-1或η≥1.
∵η~N(1,σ2),∴P(η≥1)=0.5,
又P(η<-1)=0.2,
∴P(η≤-1或η≥1)=0.5+0.2=0.7.
故答案为:0.7.
点评 本题考查了正态分布的对称性特点,函数极值点的定义,属于中档题.

练习册系列答案
相关题目
12.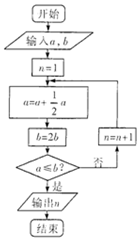 数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )
数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )
 数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )
数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-5≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,若z=ax+y仅在点(2,1)处取得最大值,则a的取值范围是( )
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
10.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-5≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,若z=3x+y的最大值是( )
| A. | 6 | B. | 7 | C. | 0 | D. | 3 |
14.下列函数中,在定义域上为减函数的是( )
| A. | y=x2 | B. | y=cosx | C. | $y={x^{\frac{1}{2}}}$ | D. | y=-lnx |
10.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于( )
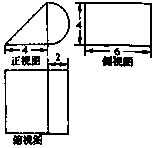

| A. | 24+6πcm3 | B. | 24+12πcm3 | C. | 48+12πcm3 | D. | 96+12πcm3 |
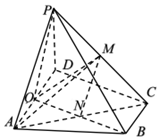 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.