题目内容
2.设函数f(x)是定义在R上的增函数,且f(x)≠0,对于任意的实数x,y都有f(x+y)=f(x)•f(y).(1)求证:f(x)>0;
(2)若f(1)=2,解不等式:f(3x)>4f(x);
(3)由(1)及题设,写出函数f(x)的一个模型.
分析 (1)由f(x)=f2($\frac{x}{2}$)可得出结论;
(2)不等式等价于f(3x)>f(2)f(x)=f(x+2),再根据f(x)的单调性得出3x>x+2,解出即可;
(3)根据函数性质可知指数函数符合f(x)的要求.
解答 解:(1)∵f(x)≠0,
∴f(x)=f($\frac{x}{2}+\frac{x}{2}$)=f2($\frac{x}{2}$)>0.
(2)∵f(1)=2,∴f(2)=f2(1)=4,
∴4f(x)=f(2)f(x)=f(x+2),
∴f(3x)>f(x+2),
∵f(x)是定义在R上的增函数,
∴3x>x+2,解得x>1.
(3)f(x)=2x.
点评 本题考查了函数单调性的应用,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
12.为了解重庆一中1800名高一学生的身体生长的状况,用系统抽样法抽取60名同学进行检验,将学生从1:1800进行编号,若已知第1组抽取的号码为10,则第3组用简单随机抽样抽取的号码为( )
| A. | 60 | B. | 70 | C. | 80 | D. | 90 |
10.学校决定把12个参观航天航空博物馆的名额给二(1)、二(2)、二(3)、二(4)四个班级.要求每个班分得的名额不比班级序号少;即二(1)班至少1个名额,二(2)班至少2个名额,…,则分配方案有( )
| A. | 10种 | B. | 6种 | C. | 165种 | D. | 495种 |
17.已知向量$\overrightarrow a=(-1,1)$,$\overrightarrow b=(3,m)$,$\overrightarrow a∥(\overrightarrow a+\overrightarrow b)$,则m=( )
| A. | 2 | B. | -2 | C. | -3 | D. | 3 |
14.某企业为了更好地了解设备改造前后与生产合格品的关系,随机抽取了180件产品进行分析,其中设备改造前的合格品有36件,不合格品有49件,设备改造后生产的合格品有65件,不合格品有30件.根据所给数据:
(1)写出2×2列联表; (2)判断产品是否合格与设备改造是否有关,说明理由.
附:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,
数据支持:(65×49-36×30)2=4431025 101×79×85×95=64430825.
(1)写出2×2列联表; (2)判断产品是否合格与设备改造是否有关,说明理由.
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
数据支持:(65×49-36×30)2=4431025 101×79×85×95=64430825.
12.某城市2014年的空气质量状况如表所示:
其中污染指数T≤50时,空气质量为优;50<T≤100时,空气质量为良;100<T≤150时,空气质量为轻微污染,则该城市2014年空气质量达到良或优的概率为$\frac{3}{5}$.
| 污染指数T | 30 | 60 | 100 | 110 | 130 | 140 |
| 概率P | $\frac{1}{10}$ | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{7}{30}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
 如图,PA=PC,∠APC=∠ACB=90°,∠BAC=60°,平面PAC⊥平面ABC.
如图,PA=PC,∠APC=∠ACB=90°,∠BAC=60°,平面PAC⊥平面ABC.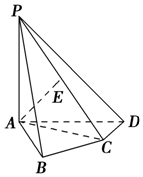 如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.