题目内容
已知方程C:x2+y2-4x-4y+a=0
(1)若方程C表示圆,求实数a的取值范围;
(2)方程C中,当a=-17时,求过点(7,-6)且与圆C相切的切线方程;
(3)若(1)中的圆C与直线l:2x-y-3=0相交于A,B两点,且OA⊥OB(O为坐标原点),求实数a的值.
(1)若方程C表示圆,求实数a的取值范围;
(2)方程C中,当a=-17时,求过点(7,-6)且与圆C相切的切线方程;
(3)若(1)中的圆C与直线l:2x-y-3=0相交于A,B两点,且OA⊥OB(O为坐标原点),求实数a的值.
考点:二元二次方程表示圆的条件,圆的切线方程
专题:直线与圆
分析:(1)由方程C:x2+y2-4x-4y+a=0配方为(x-2)2+(y-2)2=8-a,由于方程C表示圆,必需8-a>0,解得a即可.
(2)分类讨论:当切线的斜率存在时,设切线的方程为:l:y+6=k(x-7),利用直线与圆相切的性质即可得出.斜率不存在时直接得出即可.
(3)把直线l的方程与圆的方程联立可得根与系数的关系,再利用OA⊥OB?
•
=0即可得出.
(2)分类讨论:当切线的斜率存在时,设切线的方程为:l:y+6=k(x-7),利用直线与圆相切的性质即可得出.斜率不存在时直接得出即可.
(3)把直线l的方程与圆的方程联立可得根与系数的关系,再利用OA⊥OB?
| OA |
| OB |
解答:
解:(1)由方程C:x2+y2-4x-4y+a=0配方为(x-2)2+(y-2)2=8-a,
∵方程C表示圆,∴8-a>0,解得a<8.
∴a<8时,方程C表示圆的方程.
即实数a的取值范围是(-∞,8).
(2)当k=-17时,方程C为:(x-2)2+(y-2)2=25,圆心C(2,2),R=5.
∵P在圆外,∴有2条切线.
设斜率存在时切线l的斜率为 k,则 l:y+6=k(x-7),即l:kx-y-7k-6=0
由
=5,化简得 80k+39=0,解得k=-
.
∴代入l方程得其中一条切线为 l1: 39x+80y-207=0.
由图象知另一条切线为 l2:x=7.
(3)设直线l∩圆C于点A(x1,y1),B(x2,y2),
∵OA⊥OB,∴
⊥
,
∴
•
=0,
∴x1x2+y1y2=0…①
由l方程得 y=2x-3 代入方程C消去y得 5x2-24x+21+a=0,
由根与系数关系x1+x2=
,x1x2=
…②
又A,B∈l,∴y1=2x1-3,y2=2x2-3.
∴y1y2=4x1x2-6(x1+x2)+9…③,
把②③代入①得 5x1x2-6(x1+x2)+9=0,
∴5×
-6×
+9=0,
化为5a+6=0,
解得a=-
.
∵方程C表示圆,∴8-a>0,解得a<8.
∴a<8时,方程C表示圆的方程.
即实数a的取值范围是(-∞,8).
(2)当k=-17时,方程C为:(x-2)2+(y-2)2=25,圆心C(2,2),R=5.
∵P在圆外,∴有2条切线.
设斜率存在时切线l的斜率为 k,则 l:y+6=k(x-7),即l:kx-y-7k-6=0
由
| |2k-2-7k-6| | ||
|
| 39 |
| 80 |
∴代入l方程得其中一条切线为 l1: 39x+80y-207=0.
由图象知另一条切线为 l2:x=7.
(3)设直线l∩圆C于点A(x1,y1),B(x2,y2),
∵OA⊥OB,∴
| OA |
| OB |
∴
| OA |
| OB |
∴x1x2+y1y2=0…①
由l方程得 y=2x-3 代入方程C消去y得 5x2-24x+21+a=0,
由根与系数关系x1+x2=
| 24 |
| 5 |
| 21+a |
| 5 |
又A,B∈l,∴y1=2x1-3,y2=2x2-3.
∴y1y2=4x1x2-6(x1+x2)+9…③,
把②③代入①得 5x1x2-6(x1+x2)+9=0,
∴5×
| 21+a |
| 5 |
| 24 |
| 5 |
化为5a+6=0,
解得a=-
| 6 |
| 5 |
点评:本题考查了二次方程与圆的方程之间的关系、直线与圆相切的性质、点到直线的距离公式、直线与圆的相交问题转化为方程联立可得根与系数的关系、OA⊥OB?
•
=0、配方法等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.
| OA |
| OB |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设全体实数集为R,M={1,2},N={1,2,3,4},则(∁RM)∩N等于( )
| A、{4} |
| B、{3,4} |
| C、{2,3,4} |
| D、{1,2,3,4} |
已知A(-2,-2),B(4,2),点P在圆x2+y2=1上运动,则|PA|2+|PB|2的最大值是( )
| A、28 | B、30 | C、32 | D、34 |
圆心是O(-3,4),半径长为5的圆的方程是( )
| A、(x-3)2+(y+4)2=5 |
| B、(x-3)2+(y+4)2=25 |
| C、(x+3)2+(y-4)2=5 |
| D、(x+3)2+(y-4)2=25 |
在200件产品中有3件次品,现从中任意抽取5件,其中至少有2件次品的抽法有( )
A、
| ||||||||
B、(
| ||||||||
C、
| ||||||||
D、(
|
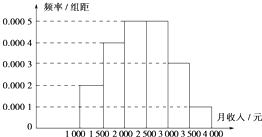 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)):