题目内容
【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
【答案】B
【解析】
先求得直线y=ax+b(a>0)与x轴的交点为M(![]() ,0),由
,0),由![]() 0可得点M在射线OA上.求出直线和BC的交点N的坐标,①若点M和点A重合,求得b
0可得点M在射线OA上.求出直线和BC的交点N的坐标,①若点M和点A重合,求得b![]() ;②若点M在点O和点A之间,求得
;②若点M在点O和点A之间,求得![]() b
b![]() ; ③若点M在点A的左侧,求得
; ③若点M在点A的左侧,求得![]() b>1
b>1![]() .再把以上得到的三个b的范围取并集,可得结果.
.再把以上得到的三个b的范围取并集,可得结果.
由题意可得,三角形ABC的面积为 ![]() 1,
1,
由于直线y=ax+b(a>0)与x轴的交点为M(![]() ,0),
,0),
由直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,可得b>0,
故![]() 0,故点M在射线OA上.
0,故点M在射线OA上.
设直线y=ax+b和BC的交点为N,则由![]() 可得点N的坐标为(
可得点N的坐标为(![]() ,
,![]() ).
).
①若点M和点A重合,如图:

则点N为线段BC的中点,故N(![]() ,
,![]() ),
),
把A、N两点的坐标代入直线y=ax+b,求得a=b![]() .
.
②若点M在点O和点A之间,如图:
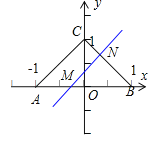
此时b![]() ,点N在点B和点C之间,
,点N在点B和点C之间,
由题意可得三角形NMB的面积等于![]() ,
,
即![]() ,即
,即 ![]() ,可得a
,可得a![]() 0,求得 b
0,求得 b![]() ,
,
故有![]() b
b![]() .
.
③若点M在点A的左侧,
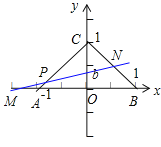
则b![]() ,由点M的横坐标
,由点M的横坐标![]() 1,求得b>a.
1,求得b>a.
设直线y=ax+b和AC的交点为P,则由 ![]() 求得点P的坐标为(
求得点P的坐标为(![]() ,
,![]() ),
),
此时,由题意可得,三角形CPN的面积等于![]() ,即
,即 ![]() (1﹣b)|xN﹣xP|
(1﹣b)|xN﹣xP|![]() ,
,
即![]() (1﹣b)|
(1﹣b)|![]() |
|![]() ,化简可得2(1﹣b)2=|a2﹣1|.
,化简可得2(1﹣b)2=|a2﹣1|.
由于此时 b>a>0,0<a<1,∴2(1﹣b)2=|a2﹣1|=1﹣a2 .
两边开方可得 ![]() (1﹣b)
(1﹣b)![]() 1,∴1﹣b
1,∴1﹣b![]() ,化简可得 b>1
,化简可得 b>1![]() ,
,
故有1![]() b
b![]() .
.
综上可得b的取值范围应是 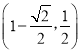 ,
,
故选:B.

【题目】某校高二年级共有800名学生参加2019年全国高中数学联赛江苏赛区初赛,为了解学生成绩,现随机抽取40名学生的成绩(单位:分),并列成如下表所示的频数分布表:
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
⑴试估计该年级成绩不低于90分的学生人数;
⑵成绩在![]() 的5名学生中有3名男生,2名女生,现从中选出2名学生参加访谈,求恰好选中一名男生一名女生的概率.
的5名学生中有3名男生,2名女生,现从中选出2名学生参加访谈,求恰好选中一名男生一名女生的概率.
【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动.某潜水中心调查了100名男性与100女性下潜至距离水面5米时是否耳鸣,下图为其等高条形图:

①绘出![]() 列联表;
列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.005的前提下认为耳鸣与性别有关系?
附:![]() ,其中
,其中![]() .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |


