Question

8．在棱长为2的正方体A₁B₁C₁D₁-ABCD中，则点B到平面A₁B₁CD的距离是$\frac{1}{2}$．

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能求出点B到平面A₁B₁CD的距离．

解答 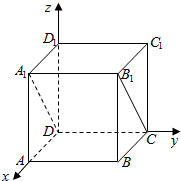解：以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
则B（2，2，0），D（0，0，0），A₁（2，0，2），C（0，2，0），
$\overrightarrow{DB}$=（2，2，0），$\overrightarrow{D{A}_{1}}$=（2，0，2），$\overrightarrow{DC}$=（0，2，0），
设平面A₁B₁CD的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{D{A}_{1}}=2x+2z=0}\\{\overrightarrow{n}•\overrightarrow{DC}=2y=0}\end{array}\right.$，取x=1，得$\overrightarrow{n}=（1，0，-1）$，
∴点B到平面A₁B₁CD的距离是：
d=$\frac{|\overrightarrow{DB}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{|2|}{2\sqrt{2}•\sqrt{2}}$=$\frac{1}{2}$．
∴点B到平面A₁B₁CD的距离是$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查点到平面的距离的求法，是基础题，解题时要认真审题，注意向量法的合理运用．