题目内容
14．已知函数f（x）是定义在（-∞，0）∪（0，+∞）上的偶函数，当x＞0时，f（x）=lnx-ax，若函数在定义域上有且仅有4个零点，则实数a的取值范围是（0，$\frac{1}{e}$）．分析 作出y=lnx与y=ax的函数图象，利用导数的几何意义得出a的临界值，从而得出a的范围．
解答 解：∵f（x）是偶函数，且f（x）有4个零点，
∴f（x）在（0，+∞）上有2个零点，
∴y=lnx与y=ax有2个交点，
作出y=lnx与y=ax的函数图象如图所示：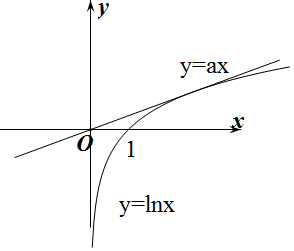
设y=ax与y=lnx相切，切点为（x0，y0），
则$\left\{\begin{array}{l}{{y}_{0}=a{x}_{0}}\\{{y}_{0}=ln{x}_{0}}\\{\frac{1}{{x}_{0}}=a}\end{array}\right.$，解得x0=e，y0=1，a=$\frac{1}{e}$．
∴当0$＜a＜\frac{1}{e}$时，直线y=ax与y=lnx在（0，+∞）上有2个交点，
故答案为（0，$\frac{1}{e}$）．
点评 本题考查了函数零点与函数图象的关系，属于中档题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1．已知x0是函数$f（x）={（\frac{1}{2}）^x}+\frac{1}{x}$的一个零点，且x1∈（-∞，x0），x2∈（x0，0），则（ ）
| A． | f（x1）＜0，f（x2）＜0 | B． | f（x1）＞0，f（x2）＞0 | C． | f（x1）＜0，f（x2）＞0 | D． | f（x1）＞0，f（x2）＜0 |
2．在△ABC中，内角A、B、C的对边分别为a、b、c，若acosB+bcosA=2ccosC，a+b=6，则三角形ABC的面积S△ABC的最大值是（ ）
| A． | $\frac{\sqrt{3}}{4}$ | B． | $\frac{9\sqrt{3}}{2}$ | C． | $\frac{9\sqrt{3}}{4}$ | D． | $\frac{9}{4}$ |
19．过点P（1，1）（且倾斜角为45°的直线被圆（x-2）2+（y-1）2=2所截的弦长是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{6}$ | D． | $\sqrt{7}$ |