题目内容
7．已知函数f（x）=-x3+2ax在（0，1]上是单调递增函数，则实数a的取值范围是（ ）| A． | （-∞，$\frac{3}{2}$） | B． | [$\frac{3}{2}$，+∞） | C． | （$\frac{3}{2}$，+∞） | D． | （-$\frac{3}{2}$，$\frac{3}{2}$） |
分析 求出函数的导函数，由函数f（x）=-x3+2ax在（0，1]上单调递增，所以f′（x）=-3x2+2a≥0在（0，1]上恒成立，分离变量后利用函数的单调性求实数a的范围．
解答 解：由f（x）=-x3+2ax，所以f′（x）=-3x2+2a，
因为f（x）=-x3+2ax在（0，1]上是单调递增函数，
所以f′（x）=-3x2+2a≥0在（0，1]上恒成立．
即2a≥3x2，在（0，1]上恒成立．
因为函数y=3x2≤3在（0，1]上恒成立，
所以a≥$\frac{3}{2}$．
故选：B．
点评 本题考查了函数的单调性与函数的导函数的关系，训练了利用分离变量法求参数的范围，考查了利用函数的单调性求函数的最值，是中档题．
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
18．已知函数f（x）=cosx，a，b，c分别为△ABC的内角A，B，C所对的边，且3a2+3b2-c2=4ab，则下列不等式一定成立的是（ ）
| A． | f（sinA）≤f（cosB） | B． | f（sinA）≤f（sinB） | C． | f（cosA）≤f（sinB） | D． | f（cosA）≤f（cosB） |
15．$\frac{tan（3π-α）}{{sin（π-α）sin（\frac{3π}{2}-α）}}+\frac{{sin（2π-α）cos（α-\frac{7π}{2}）}}{{sin（\frac{3π}{2}+α）cos（2π+α）}}$化简的结果是（ ）
| A． | -1 | B． | 1 | C． | 0 | D． | $\frac{1}{{{{cos}^2}α}}$ |
17．
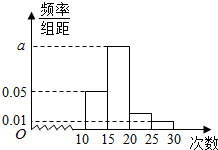某校对高一年级学生暑假参加社区服务的次数进行了统计，随机抽取了M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如下：
（1）求表中n，p的值和频率分布直方图中a的值，并估计该校高一学生参加社区服务超过20次的概率；
（2）试估计该校高一学生暑假参加社区服务次数的中位数．
某校对高一年级学生暑假参加社区服务的次数进行了统计，随机抽取了M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如下：| 分组 | 频数 | 频率 |
| [10，15） | 10 | 0.25 |
| [15，20） | 25 | n |
| [20，25） | m | p |
| [25，30） | 2 | 0.05 |
| 合计 | M | N |
（2）试估计该校高一学生暑假参加社区服务次数的中位数．