题目内容

2．已知p：1是集合{x|x2＜a}中的元素，q：2是集合{x|x2＜a}中的元素．当p或q是真命题时，求a的取值范围．

分析 先求出命题p，q同时为真命题的条件，然后进行求解即可

解答 解：若1是集合{x|x2＜a}中的元素，则1＜a，即a＞1，即a的取值范围为（1，+∞）
若2是集合{x|x2＜a}中的元素．则a＞4，即a的取值范围为（4，+∞），
若当p或q是真命题时，则p，q至少有一个为真命题，
则满足（1，+∞）∪（4，+∞）=（1，+∞）．
即a的取值范围是（1，+∞）

点评 本题主要考查复合命题真假关系的判断和应用，求出命题的等价条件，结合集合的并集关系是解决本题的关键．

练习册系列答案
相关题目
12．二次函数f（x）满足以下条件：①f（x+2）=f（2-x）；②最小值为-8；③f（1）=-6
（1）求f（x）的解析式；
（2）求函数f（x）在区间（-1，4]上的值域．
13．若a＜b＜0，则下列不等式：①|a|＞|b|；②$\frac{1}{a}＞\frac{1}{b}$；③$\frac{a}{b}+\frac{b}{a}＞2$；④a2＜b2中，正确的有（　　）
A．1个B．2个C．3个D．4个
10．在△ABC中，a=4，b=$\frac{5}{2}$，cos（A-B）cosB-sin（A-B）sin（A+C）=$\frac{3}{5}$，则角B的大小为（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{5π}{6}$
17．设函数$f（x）=2cos（\frac{π}{3}-\frac{x}{2}）$，
（1）求f（x）的周期；
（2）当x∈[-π，π]时，求f（x）单调递增区间；
（3）当x∈[0，2π]时，求f（x）的最大值和最小值．
7．已知函数f（x）=-x3+2ax在（0，1]上是单调递增函数，则实数a的取值范围是（　　）
A．（-∞，$\frac{3}{2}$）B．[$\frac{3}{2}$，+∞）C．（$\frac{3}{2}$，+∞）D．（-$\frac{3}{2}$，$\frac{3}{2}$）
14．设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a1+b2=3，a2+b3=7
（Ⅰ）求{an}，{bn}的通项公式；        
（Ⅱ）求数列$\left\{{\frac{a_n}{b_n}}\right\}$的前n项和Sn．
11．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的离心率为$\frac{{2\sqrt{3}}}{3}$，若抛物线C：y2=2px（p＞0）的焦点F到双曲线的渐近线的距离为1，
（1）求抛物线C的方程；
（2）过点F的直线l交抛物线C于A、B两点（点A在x轴下方），若$\overline{AF}=\frac{1}{3}\overline{FB}$，求直线l的斜率．
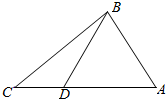12．如图，在△ABC中，sin$\frac{∠ABC}{2}$=$\frac{\sqrt{3}}{3}$，AB=2，点D在线段AC上，且AD=2DC，BD=$\frac{4\sqrt{3}}{3}$．
（Ⅰ）求cos∠ABC；
（Ⅱ）求BC和AC的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网