题目内容
5.已知数列{an}的前n项和为Sn,且a1=$\frac{1}{2}$,an=-2SnSn-1(n≥2),则S200=$\frac{1}{400}$.分析 an=-2SnSn-1化简可得$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,且$\frac{1}{{S}_{1}}$=2,从而可判断数列{$\frac{1}{{S}_{n}}$}是以2为首项,2为公差的等差数列,从而求得.
解答 解:∵an=-2SnSn-1,
∴Sn-Sn-1=-2SnSn-1,
∴$\frac{1}{{S}_{n-1}}$-$\frac{1}{{S}_{n}}$=-2,
即$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,且$\frac{1}{{S}_{1}}$=2,
故数列{$\frac{1}{{S}_{n}}$}是以2为首项,2为公差的等差数列,
∴$\frac{1}{{S}_{n}}$=2+2(n-1)=2n,
故Sn=$\frac{1}{2n}$,
故S200=$\frac{1}{400}$,
故答案为:$\frac{1}{400}$.
点评 本题考查了数列的性质的判断与应用,同时考查了整体思想与转化思想的应用及构造法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.“m>2”是“函数f(x)=m+log2x(x≥$\frac{1}{2}$)不存在零点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
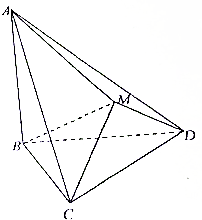 如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.
如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.