题目内容
16.已知△ABC的外心为O,且2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,则cos∠BAC的值是$±\frac{1}{4}$.分析 利用向量的运算得出4|$\overrightarrow{OA}$|2=9|$\overrightarrow{OB}$|2+16|$\overrightarrow{OC}$|2+24$\overrightarrow{OB}$$•\overrightarrow{OC}$,再利用外接圆得出4R2=25R2+24R2cos∠BOC,cos∠BOC=-$\frac{7}{8}$,
最后利用圆的几何性质,二倍角公式求解即可.
解答 解:∵△ABC的外心为O,且2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,半径为R
∴-2$\overrightarrow{OA}$=3$\overrightarrow{OB}$+4$\overrightarrow{OC}$,
平方得出:4|$\overrightarrow{OA}$|2=9|$\overrightarrow{OB}$|2+16|$\overrightarrow{OC}$|2+24$\overrightarrow{OB}$$•\overrightarrow{OC}$
∴4R2=25R2+24R2cos∠BOC
cos∠BOC=-$\frac{7}{8}$,
∵根据圆的几何性质得出:∠BOC=2∠BAC,
-$\frac{7}{8}$=2cos2∠BAC-1,
∴cos∠BAC=$±\frac{1}{4}$
故答案为:$±\frac{1}{4}$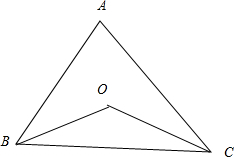
点评 本小题主要考查三角形外心的应用、向量在几何中的应用等基础知识,考查运算求解能力与转化思想.属于基础题

练习册系列答案
相关题目
4.已知函数f(x)的定义域为R,且f′(x)+f(x)=2xe-x,若f(0)=1,则函数$\frac{f′(x)}{f(x)}$的取值范围为( )
| A. | [-2,0] | B. | [-1,0] | C. | [0,1] | D. | [0,2] |
8.等差数列{an}中,若a5=7,则( )
| A. | S9=63 | B. | S11=63 | C. | S9=35 | D. | S11=77 |